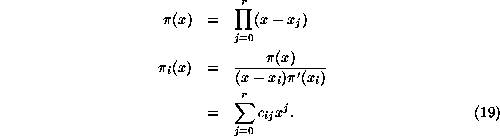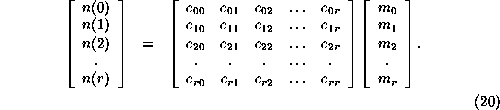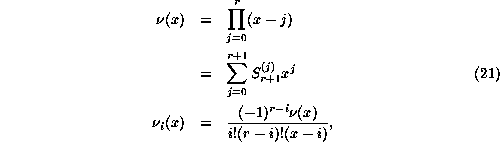Moments and frequencies
A distribution of data is characterized by its collection of moments as well as by the
individual frequencies with which the data occur; these are really two complementary
aspects of the same data set. Here, frequencies 
are associated with the nonnegative integers i, namely the number of configurations
with a given number of ancestors. The 
moment of
this data is defined by
where it is understood that 
.
The second volume, second edition of William Feller's popular book on the theory of probability [31] contains some material on moments; an advanced theory can be found in the American Mathematical Society Survey written by J. A. Shohat and J. D. Tamarkin [32].
Regarding the right hand side of Eq. 18 as the inner product of two vectors, then displaying the equations for individual moments, reveals a matrix equation
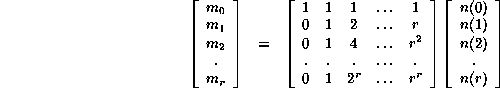
expressing the moments in terms of the frequencies. One desires a reversed relation, expressing frequencies using moments, the more so supposing that the moments could be calculated independently. Naturally this requires the determination of as many moments as frequencies, in order to produce a square matrix for inversion.
The matrix shown is a particular case of a type which is very well known in mathematics, the Vandermonde matrix. Its general form is
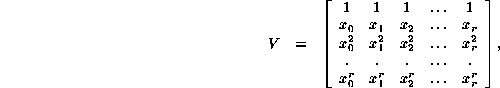
readily invertible through the use of the Lagrange interpolation polynomials 
, defined by
The inverse matrix transforms moments into frequencies: 0.30em
It is important to appreciate the mechanism by which the product 
yields the identity matrix. There are r+1 interpolation
polynomials to evaluate at r+1 points; each polynomial vanishes at all the
``wrong'' points, while assuming unit value at the ``right'' point, namely the one for
which the subscripts match. The matrix 
contains
rows of coefficients for such polynomials; in the matrix product they form inner products
with the columns of V, composed of all the powers needed to evaluate the polynomial
at some particular point. The resultant interplay of right and wrong creates the unit
matrix.
Because the ancestral data is all evenly spaced, the interpolation polynomials
specialize to the Newton polynomials 
,
whose characteristics have been nicely described, for example in Berezin and Zhidkov's
numerical analysis text [33]. The primary polynomial 
is symmetric or antisymmetric with respect to 
according to its parity, oscillating with diminishing
amplitude from the origin to the midpoint, and growing rapidly outside the interval 
.
The coefficient 
in Eq. 21 is a Stirling number of the first kind, as described in
Abramowitz and Stegun's mathematical handbook [34]. The
explicit formula cited therein is fairly long; asymptotic formulas, some special values
and tables are also presented.
Since we have already seen how to express the moments of the counterimage distribution in terms of tensor powers of the de Bruijn fragments, we have an alternative viewpoint from which to examine the frequency of counterimages.
An important special case is that of zero variance, in which all data equal x,
say; in that case one would have 
, for which the
inversion formula Eq. 20 would yield 
. Supposedly x would be an integer, so that x's actual
frequency r+1 would be recovered, all other frequencies vanishing. Nevertheless the
formula is valid for any sequence of moments which are powers of x, such as might
arise from an eigenvalue of one of the tensor power sums.
In practice, the high moments of any distribution are dominated by the largest datum;
accordingly we might expect the inversion of a moment distribution to involve the maximal
frequency plus a tail composed of the lower moments weighted by coefficients from the
upper left hand corner of the matrix 
. These
coefficients approach limiting values for large values of r, which would be the
case of principal interest; moreover they diminish factorially while the moments increase
as powers, ensuring convergence. For example, combining Equations 19
and 21 yields the frequency 
corresponding to the Garden of Eden,
We have just seen that 
vanishes (no Garden of
Eden) for distributions with zero variance; the converse would be that it only
vanishes for zero variance, a conclusion whose likelihood is greatly enhanced by the
existence and appearance of Eq. 22.
Harold V. McIntosh
E-mail:mcintosh@servidor.unam.mx