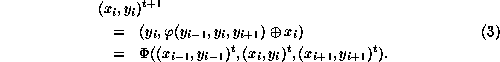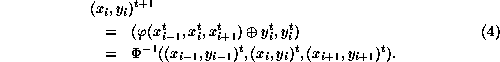Cartesian product rule

Toffoli's own scheme [21] increases the dimensionality of the automaton rather than the number of generations spanned by its evolutionary rule. However, the simplest solution to the problem of exhibiting explicitly reversible rules of evolution may well lie in increasing the number of states of the automaton, by forming their cartesian products, whose rule of evolution needs to span but a single generation:

 

Thus a single cell of a automaton may hold two successive generations of a automaton by forming pairs whose components are to be interpreted as

substitution of these values into Eq. 3 reproduces Eq. 1, in its turn reversible by the rule

 

Similar formulas would allow the formation of reversible rules from arbitrary rules, the more so by taking advantage of additional alternatives for . Nor is it difficult to invent schemes whereby the equivalent of three generations of evolution could be incorporated into automata, and so on and on for even longer histories.

To understand possible complications which can arise, consider Fredkin's idea applied to a automaton via a rule in which sequential letters replace subscript indices for improved legibility:

Evolution loses the value of c, preserves d intact, yet permits the recovery of a if b were known explicitly. Supposing a third cell provides two cells in the second generation,

from which c can now be recovered via with the aid of the explicitly known d and f. Since d is already known, the cell has been reconstructed, as could be done for all the rest of the cells of a configuration.

In each case evolution ``remembers'' the second component of the right cell, but the left ancestor is the one recovered by the reversed rule. Typical of neighborhoods with half integral radius, this asymmetry seems to have no further significance. It is often seen in rules with shifting.

---

Harold V. McIntosh
E-mail:mcintosh@servidor.unam.mx