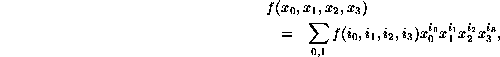
Their simplest description is through four boolean functions, one for each plane, which in turn are functions of four boolean variables, likewise the values of the cells in each plane. Either of the Shannon canonical forms would give a concise description of such a function; for example
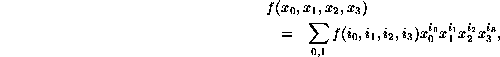
wherein the sum represents boolean , the boolean AND is implicit, and superscripts differentiate between complementation (0) or not (1).
Some functions are considerably simpler than their canonical form, which is nevertheless a good representation to use.
To describe the canonical form, each of the sixteen coefficients must be specified for each plane; strictly speaking, each one should be binary, but hexadecimal coefficients could be used for economy of representation. The coefficients of all four planes could be combined to give a single sequence of sixteen hexadecimal numbers; alternatively, each individual plane could get a four digit hexadecimal number, which would be more compatible with defining separate rules for each of the bitplanes.
The function inhx(f), whose argument int f[4][16] is
composed of the four coefficient vectors, installs a 
automaton
in the CAM
(with a zero alternative), assisted by the table
generating function shancf which has some additional arguments
which are not visible to the user of inhx.