Consider the same graphs,
![]()
representing a digon, and
![]()
representing a triangle. The loops of the first have length 2, those of
the second, length 3. It would seem that loops common to the two would
have length 6; what is the diagram which would express this fact? The
evident candidate is the cartesian product of the two graphs, linkage
between its points occurring only if both coordinates were linked, for
which we use the symbol ![]() .
.
![]()
Effectively, linkage in the cartesian product is defined by
![]()
In this example, the intersection has nodes
![]()
with links
![]()
![]()
Graphed by usual conventions, a folded hexagon results, manifesting the required cycle of length 6, as seen in Figure 2.
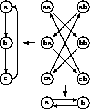
Figure 2: Greatest lower bound of a digon and a triangle.
The topological matrix of the intersection of two diagrams is the tensor product of the topological matrices of the constituents.