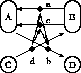
Figure 6: The antidual of a diagram lets nodes be links.
Going in the other direction, it would be nice to know when the CR factorization is possible, independently of whether RC was available for comparison or not.
The rules of matrix multiplication are such that when R is used as a left factor, it simply rearranges the rows of the left factor. Thus in any product RA=N, A would have the same rows as N. But if A were of type C, different rows would have to have their ones in different columns, a restriction which could be summarized by saying that the rows were orthogonal. Consequently the rows of N would have to be either identical or orthogonal; lacking this characteristic it could not have an RC factorization. Conversely, dual diagrams necessarily show the evidences of such a composition.
Given the necessary conditions, factors R and C can be constructed; a lack of uniqueness will be evident in some of the steps. To begin with, C must have at least the distinct rows of N (including a zero row if necessary) arranged in some order. But if N has one or more columns of zeroes, some rows containing ones must be provided lest C be nonstochastic.
The final number of rows chosen determines the number of columns of R, which is filled in at last by placing the rows of C in their proper place in N. Zero rows in N must be created by copying a row from C---not using zero coefficients in R---in order to keep R stochastic.

Figure 6: The antidual of a diagram lets nodes be links.
If the diagram of Figure 5 is given this treatment, we find the antidual shown in Figure 6, calculated as follows:
0.4em
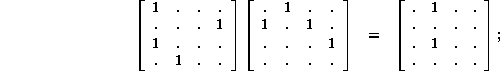
reversing the order yields the graph to which it is dual:
0.4em
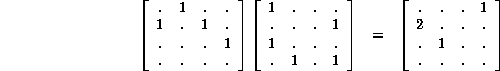
Interestingly, this antidual contains a double link, whose importance is evident from Figure 6.
For a thorough presentation of duals, which they call ``line graphs,'' Robert Hemminger and Lowell Beinecke's survey [5] should be consulted. Among other things they cite criteria which avoid the presence of self-loops and multiple links in the dual diagram. Essentially there is a list of configurations such as the example presented here, which have to be avoided. The dichotomy ``identical or orthogonal'' which figures in the construction of the antidual was formulated by Paul Richards [6] in 1967.