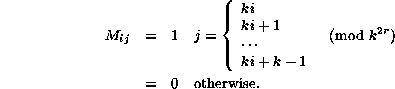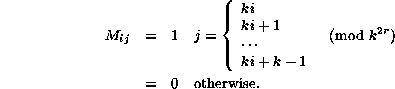
The nodes of the de Bruijn diagram are sequences of symbols from some alphabet, just as regular expressions are. They can even be sequences of nodes from a specific graph. The links of the diagram describe how such sequences may overlap. Different degrees of overlap lead to different diagrams, the simplest of which overlap according to the gain or loss of a single initial or terminal symbol. Thus the binary sequence 0011 overlaps the sequence 0110 by losing 0 as its initial symbol, whereas the second sequence overlaps through the loss of 0 as a terminal symbol. The link can be labelled according to the displaced symbol, as well as by the composite sequence 00110, and a variety of other ways. The intended application generally governs the choice.
When the symbols are consecutive integers they can be treated as elements of a ring or perhaps a finite field; the ease of discussing their properties arithmetically or algebraically makes the choice eminently worthwhile. For example, the topological matrix of a de Bruijn diagram becomes simply