To illustrate the use of the subset diagram, consider the automaton for
Rule 126:
.1em
In other words, all neighborhoods evolve into ones with the exception
of 111 and the quiescent neighborhood 000, which evolve into zeroes. The
de Bruijn diagram for this rule is 
, which has the symbolic
variant (dots represent the null word 
):
0.50em
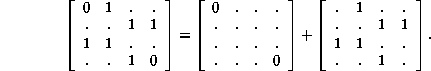
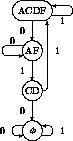
Figure 13: Subset diagram for Rule 126.
Since the nodes A=00, C=01, D=10, and F=11 are linked by the
symbols 0 and 1, the subset diagram can be constructed. It actually has
nodes for the sixteen subsets, but to save space we show only the
part connected to the full subset (
is the empty set). First,
note the destination of each arrow leaving individual nodes:
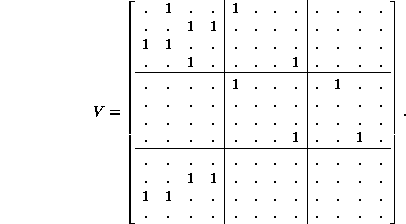
Then, form vectors whose elements are the tail nodes and whose components are indexed by the head nodes; an element is null if there is no incoming link from any node.
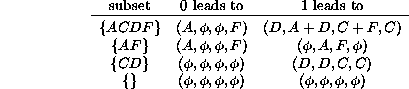
This structure is actually the vector subset diagram; the scalar subset diagram arises by enumerating the non-null indices (we don't care how many incoming arrows there are nor where they originate, as long as there is at least one):
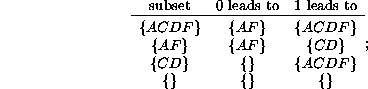
its topological matrix, having indexed the subsets in the order shown, is S=a+b according to
0.50em
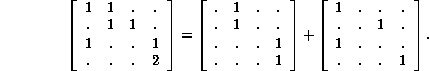
The matrix is upper triangular, because the null set is linked only to
itself. Only the 
submatrix in the upper left hand corner
is really necessary. The 2 in the lower right corner is not strictly
required, attesting only to the fact that no path from the null
set has anywhere else to go, thereby conserving the uniform row sum.
Finally, the topological matrix of the vector subset diagram is
