A vector subset diagram whose links have been labelled according to the evolution of an automaton allows the gathering of fairly subtle information. Its powers classify the counterimages they are counting exactly by initial and terminal partial neighborhoods, in addition to lumping them into subsets as the scalar matrix does.
Often this is a more elaborate classification than is needed; what really count are the de Bruijn fragments comprising the submatrices, classifying ancestors according to their initial and final partial neighborhoods. Generally further sorting by subsets of partial neighborhoods only serves to identify and count the Garden of Eden configurations quickly.
For example, continuing to use the example from Rule 126, the de Bruijn
product for the sequence 
is
0.50em
which makes it clear that an infinite quiescent configuration
has exactly two ancestors, itself and 
; in any event, 01 and 10 are
excluded both as initial sequences and as final sequences from finite
configurations such as on a ring. Of course, this information can also
be elicited from the scalar subset matrix by looking at all the paths
originating from unit classes.
Counterimages can be counted three ways: quiescent at infinity, cyclic,
or completely general. Let 
be a typical product of de Bruijn
fragments generating the counterimages of a configuration; then
where q is the completely quiescent partial neighborhood, yields the
number of counterimages quiescent at infinity. The single nonzero element
of the projection operator 
occupies the qth position on the
diagonal; the trace formulation provides a uniformity of treatment for
all three cases.
For a cyclic automaton, it is appropriate to recognize that a cycle must begin and end on the same partial neighborhood by calculating (for unit matrix I)
Finally, the appropriate unrestricted formula would be
where u is a vector, U a matrix, solidly filled with 1's. In fact, all three counts can be described by either a trace or an inner product, both of which are linear functionals for matrices.
Taking into account all possible products representing ancestors of a configuration of length n requires evaluating
but a+b=D, the de Bruijn matrix which satisfies DU=kU and
. Altogether, then,
The unsurprising average of ancestors per configuration being 
,
whenever some configuration has fewer, another must have more. When the
imbalance is sufficiently severe, Garden of Eden configurations are
required to compensate the configurations with multiple ancestors---a
trivial result for finite automata but with interesting consequences
for infinite automata.
The second and higher moments of the distribution of counterimages can
be obtained from some additional matrix algebra. In the following
sequence of substitutions, let P be one of the 
(noncommuting)
factors in the expansion of 
.
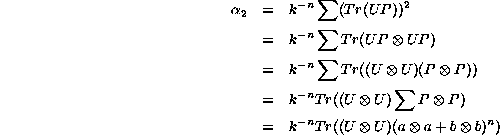
If 
is the dominant eigenvalue of 
, a
term proportional to 
will result for large n.
Higher moments will depend on higher tensor powers of a and b,
while the same formula persists with a suitably subscripted 
and
; for example
In another direction, if the connectivity matrix had been decomposed into three classes of links a, b, and c, the second moment would have taken the form
