Although the zeta function was not always given that name, there is a classical relationship between it, the characteristic polynomial, and the traces of the powers of a matrix, which are simply restatements of certain properties of polynomials. By convention, the characteristic polynomial of the matrix M is defined to be the determinant
which is equivalent to
for eigenvalues 
. Written as a polynomial in powers of t,
wherein the coefficients 
can be expressed either as homogeneous
products of the roots 
or as sums of principal minors, both
according to well known formulas.
For the transformations which we intend to make, it is more convenient to
use 
as a variable or, to avoid confusion, to introduce the function
whose factored form is
As a polynomial it differs from 
only in attaching the
coefficients 
to ascending rather than descending powers of t:
Both 
and 
are finite polynomials, whose reciprocals could
be represented as power series, even treating them formally and ignoring
questions of convergence. We are interested in 
as the
reciprocal of 
,
which can be represented as a single power series by representing each factor in the denominator as a geometric series, multiplying them term by term, and collecting coefficients.
In that case
where 
is the sum of all possible homogeneous products of
; when n=2, for instance,
.
Of more interest are the coefficients of 
for which
in other words, the traces of the powers of M.
The practical situation is that the coefficients 
are always
fairly easy to obtain, while the quantities that are really desired are
either the coefficients 
or 
. Comparison of the series
involved in each of the definitions yields equations of convolution
type relating the coefficients, typically in the form of single
determinants. Recovering the eigenvalues from the coefficients is much
harder since that is just the problem of finding the roots of a
polynomial; all the same, the task is hard to avoid since it is likely
that some or all of the eigenvalues will be sought for.
Newton's identities relate the power sums 
to the coefficients
of the characteristic polynomial; in the present context they
are obtained by differentiating the formula 
to
obtain 
. Comparing coefficients
yields the convolution (with 
)
which can be solved for either a or m in terms of the other.
For example, the system of equations
is readily solved for the a's, to obtain
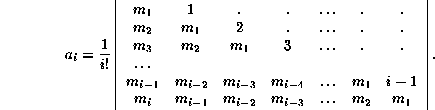
For example,
,
.