It is rare that we will find a matrix which meets the non-redundancy
criterion for all of its cycles, so consideration should be given
to the contrary case. The situation is nicely illustrated for the
de Bruijn matrices, which have cycles of all possible varieties while
still retaining a certain amount of systematic order. The shift-register
interpretation of a de Bruijn matrix makes it clear that an n-stage
matrix will have 
distinct cycles; but those which possess
translational symmetry will be redundant. For example, a cycle of 5
zeroes will show up only once in the fifth power of a two-stage matrix,
whereas the string 11010 will show up five times and be counted as one
single loop in evaluating 
There would appear to be two alternatives: either insist that the name ``zeta function'' refer exclusively to the generating function which counts loops although it might not incorporate the resolvent, or retain the elegance of the resolvent even though it may not always count loops correctly. It would appear that the latter alternative is the one that is generally chosen; moreover that such a definition was implicit in classical treatments of the theory of equations even though such a name was never used explicitly.
Since we know the characteristic equation of a finite de Bruijn matrix, it is a straightforward matter to see that they all have the same zeta function
from which we obtain
as the ``number of cycles'' of length k, although we know that this is in no way a natural representation of the true state of affairs. At least for de Bruijn matrices, we can get some idea of the discrepancy; using the probabilistic de Bruijn matrix produces an even more general result.
Beginning with the two stage matrix whose elements incorporate both a
probability and the parameter t 
,
we have
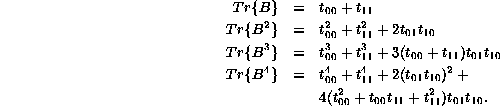
On the other hand if we work with the three stage matrix,
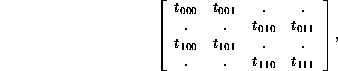
we have
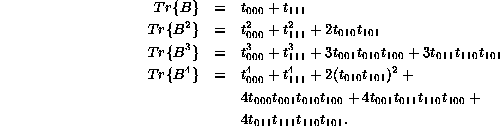
The first thing to be observed is that the structure of these matrices
is quite similar, thanks to the fact that the de Bruijn matrices form a
very regular family. In fact the same cycles will reappear in all the
trace formulas, the only difference being the length of the overlappable
fragment represented in each subscript. For example, 
will
always be the sum of two contributions, one for the string 
and
the other for the string 
; likewise a contribution from these
two strings and another from 
will always appear in
.
Another observation, although it is just barely evident from the small
number of terms that have been written, is that the series can be
rearranged to group the terms belonging to one particular cycle into
its own logarithmic series. It is clear that the terms 
and
in the first example can be so arranged. There is an
indication that the term 
would participate in another,
since the factor 2 cancels opportunely wherever it occurs.
Recalling the shift register interpretation of de Bruijn diagrams, we
see that every cycle which has no internal translational symmetry will
show up k times in 
only to be divided by k in the
term 
. If there is an internal symmetry present,
the unit cell will have length 
; its cycle will occur to the power
, but will only be 
such terms in the trace. Note how
has coefficient 2, not 4, in 
, or
that 
only has coefficient 1.
The series for 
belonging to the two-stage de Bruijn matrix could
then be rearranged to take the form
In turn this produces a zeta function
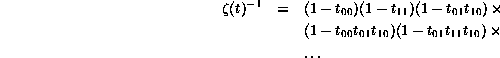
This is a very beautiful and elegant formula, and also blatantly at odds with the fact that B has only two eigenvalues, its characteristic polynomial can only vanish for two values of t, and that its zeta function should have at most two poles. Clearly it is a formula which does not meet the requirements for a convergent infinite product.