The zeta function approach is useful for determining the characteristic equation of a matrix, or even of a family of matrices with a similar structure. Its best application lies in contexts where the parameters associated with all cycles beyond a certain length are known to be negligible, or at least thought to be so. Information about eigenvalues and quantities derived from them is available, but eigenvectors are beyond the scope of the zeta function. Since reciprocal eigenvalues determine the poles of the zeta function, it would seem to be best suited for determining the first few of the largest eigenvalues of a family of matrices.
The reduced evolution matrix has a constant column sum, so its largest eigenvalue is a foregone conclusion. The equilibrium eigenvector is an object of interest, but cannot be encountered via the zeta function. The second largest eigenvalue determines the stability of equilibrium, making it a worthwhile quantity to determine.
The non-zero elements 
of the reduced evolution matrix are
those for which there are cells i and j for which 
.
Diagonal elements must therefore satisfy
and therefore are given by the number of ways that x is surrounded by acceptable neighbors; but in any event are determined by the still lifes.
Diagonal elements of 
are those for which
so that if there is a cycle of length two, there will be a corresponding diagonal element. Continuing the analysis, it is clear that there will be diagonal elements in the powers of E for all the periods whose cycle is equal to the block length. The fact that the least pole of the zeta function is known will exercise a certain restraint on the possible values which the cycle probabilities can assume.
It is in the nature of a reduced evolution matrix that the actual cycles will not just be counted, but overcounted to the extent that they can be broken open and embedded in a larger neighborhood whose central segment follows the same cycle; such is the influence of the dangling cells in the formulas above. Nevertheless this discrepancy is expected to diminish as longer blocks are used, or if the reduced evolution matrix for iterated evolution were used.
Let us work out some of the reduced evolution matrices for Wolfram's (2,1) Rule #22: Its symbolic de Bruijn matrix is
giving the two matrices
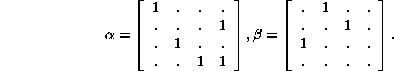
from whose products the number of counterimages of any given configuration can be determined. These products give directly the row sums of the reduced evolution matrix, but the individual matrix elements have to be worked out on their own account. Evolution matrices describe evolution differently, sorting counterimages by their central strings, rather than by the cells with which they begin and end.
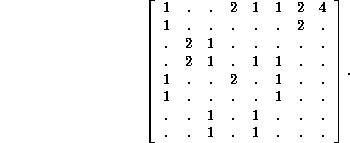
The reduced evolution matrix for 1-blocks is
The zeta function is
For 2-blocks it is
with the same zeta function, in which the presence of two zero eigenvalues is not visible
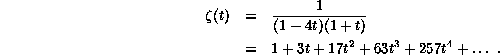
For 3-blocks it is
