Before feeling unduly discouraged about the discrepancy between the
apparent number of poles of the zeta function and the dimension of its
matrix, we should examine the zeta function more carefully. Since we
know the exact zeta function for the normal de Bruijn matrix B, all
of whose non-zero matrix elements have the form 
, we would
want to examine
The limit expression for the zeta function is exactly the one that was expected, although truncating the product representation or otherwise taking it too literally leads to the appearance of spurious poles. Although the algebra is slightly more complicated for the probabilistic matrix, multiplying out the factors of the zeta function reproduces the characteristic polynomial for the general case just as well as it does for the normal case. In principle it must be possible to reconstruct the factored form of the characteristic polynomial, but to do so directly is little more than an exercise in going around in circles. Instead we should utilize the fact that the zeta function has been described in terms of cycles of matrix elements.
The difference between primitive and composite cycles is an important
one. A cycle is primitive when its translational symmetry is trivial.
Composites are aggregates of primitive cycles, not necessarily connected
to one another. Thus, for a two stage diagram 
,
joins into one long cycle with repeated nodes; but in a three stage
diagram the analogous 
forms two disconnected
cycles. Because their primitive cycles are selfcontained and independent,
composites are commutative, but they never contain repeated factors.
Let c stand for a product of matrix elements forming a cycle, such as
and let C be a composite cycle, such as
. Let |C| denote the total length of the
composite, but let 1 be the composite cycle of length 0. Finally, let
be the parity of the composite cycle, which is required to
expand the product of differences.
If a three-valued definition of parity is used, making it vanish for
composites with repeated factors; and taking it to be unity for the
null composite, 
is the classical Möbius function redefined
for cycles:
Then, according to the distributive law, the product
can be replaced by a sum
If the composites are grouped by length, the sum presents once again the form of a polynomial:
If the dimension of B were finite, we would expect all the terms of high degree in this sum to vanish. For example, the terms with |C|=3 belonging to the two-stage de Bruijn matrix are
which evidently vanishes. The corresponding term for the three-stage matrix is
which need not.
Thus we have a scheme which is capable of displaying the structure of the characteristic polynomial of a matrix explicitly in terms of loops formed from the elements of the matrix. Nevertheless, the same results would also have followed from a careful analysis of the characteristic determinant, although the assignment of parity to the terms is phrased in a somewhat different form.
Using subscripts to identify the cycles by their lexicographically ordered repeating unit, the zeta function for binary de Bruijn matrices takes a form independent of the number of stages, namely
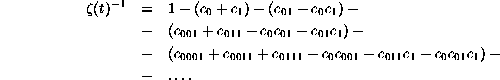
When it is no longer possible to find long cycles which are not composites of shorter cycles, it may be concluded that the series represents a matrix of a finite number of stages; otherwise there is no intrinsic limitation on the series.
The parameters upon which this series depends are no longer the probabilities of individual links in the diagram, but rather the collective probabilities belonging to the primitive cycles. There is also a tendency to disguise the contribution of the block determinants to the zeta function, but this simply means that we have a complementary approach to its interpretation.