Let us continue with , likewise labelling its rows and columns by the 2-blocks to which they correspond. Zero matrix elements---for which there is no link in the de Bruijn diagram---will be suppressed in favor of dots.

.3em

 
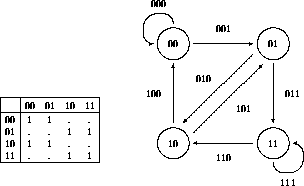
Figure: Two stage binary de Bruijn matrix and diagram. 

By a simple calculation,

which is a minimal equation rather than a characteristic equation since it is not of degree 4. Its roots are . is evidently singular because of the repeated rows, but on closer inspection we find that it shows the Jordan canonical form with respect to a block belonging to eigenvalue 0.

The matrix of principal vectors reducing to canonical form could be

The first three columns are eigenvectors, the last a principal vector.

Although characteristics of the de Bruijn matrices are already evident in , it is worth going on to examine for good measure.