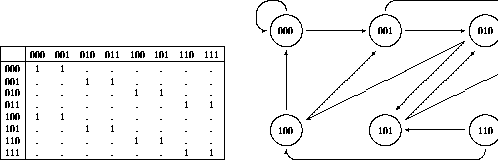
Figure: Three stage binary de Bruijn matrix and diagram.
.1em

Figure: Three stage binary de Bruijn matrix and diagram.
This time the minimal equation is
![]()
The
general result is that ![]() is a
is a ![]() matrix whose
minimal equation is
matrix whose
minimal equation is
![]()
and which exhibits the Jordan canonical form for k > 2.
This result shows that it takes at most n links to get from one node to another in an n-stage de Bruijn diagram; in terms of shift register sequences this is precisely the shift required to completely replace one sequence by another. If the node labels have internal symmetry, a smaller shift and hence a shorter path through the diagram may exist.
Although the form of the minimal equation can be conjectured readily enough by inspection, an instructive proof can be given, whose elements will be useful later on. We begin with two factorizations of the de Bruijn matrix, motivated by the observation that it would be block diagonal if only its rows were rearranged.