As an example, consider Rule 22. For brevity, label the nodes A, C, D, F. They are linked by zeroes and ones according to the following table:
The links are not evenly distributed between zeroes and ones; indeed there are five zeroes and three ones so there just couldn't be a balance. In this case the discrepancy shows up at node F, which will surely cause trouble.
Figure 
shows the connections between the subsets of the
initial subset {A C D F}, and the resulting subset diagram. Note that
the penultimate row, containing the unit classes, almost reflects the
de Bruijn diagram, except where the imbalance in links results in a
link descending to the empty set or rising to a higher level (which can
only be to the row of doublets, for a binary rule).
.1em
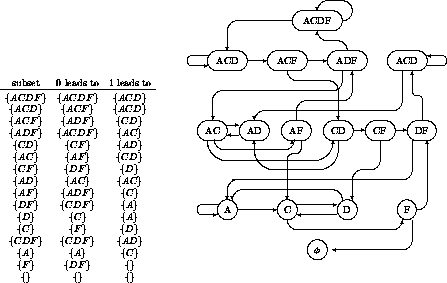
Figure: The subset diagram (exit links) for Rule 22.
It seems that all sixteen subsets have to be used to complete the analysis. It also appears that both 10101001 and its reverse, 10010101, lead directly to the null set, so they are both excluded words; the shortest ones that can be found for Rule 22.