Rule 18, whose statistical properties have been extensively studied by Grassberger, is very similar to Rule 22, except for the fact that single cells die out rather than remaining to affect further evolution. The consequence is that isolated cells form growth clusters whose interiors die out, just as for Rule 22. However, the fate of colliding frontiers from two different clusters depends on the parity with which they collide, and as a result the evolution of Rule 18 is largely characterized by the conflict of neighboring domains of opposite parity. Occasionally a domain will shrink and disappear, allowing its two neighbors to coalesce. Grassberger was interested in the random walk involved.
The following script shows the subset machine for Rule 18.
(2,1) Rule #18 Like LIFE but single cells die (00*(0+10*1))* Transitions from original machine Node A: Link 0:(A ) Link 1:(C ) Node C: Link 0:(D F ) Link 1:(% ) Node D: Link 0:(C ) Link 1:(A ) Node F: Link 0:(D F ) Link 1:(% ) Transitions from subset machine Node ADF: Link 0:(ACDF ) Link 1:(AC ) Node CDF: Link 0:(CDF ) Link 1:(A ) Node A: Link 0:(A ) Link 1:(C ) Node DF: Link 0:(CDF ) Link 1:(A ) Node : Link 0:( ) Link 1:( ) Node C: Link 0:(DF ) Link 1:( ) Node AC: Link 0:(ADF ) Link 1:(C ) Node ACDF: Link 0:(ACDF ) Link 1:(AC )
The next script shows the symbolic equation set of the subset machine
for Rule 18. (The nodes have been relabelled according to 
,
, 
, 
, 
, 
, 
,
)
a=a.0+c.0+% b=a.1+c.1 c=b.0 d=b.1+g.1 e=d.0 f=e.0+f.0 g=e.1+f.1+g.0 h=d.1
Since there are relatively few equations, we can write their symbolic
coefficient matrix fairly easily. By partitioning it into submatrices
certain characteristics of the equations are emphasized; namely that
certain groups of nodes are selfcontained. Links lead into the group
but there are no links leading out again. Figure 
shows the
coefficient matrix (assuming the nodes to form a column vector) and the
part of the subset diagram derived from the full subset.
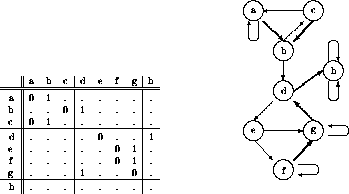
Figure: Subset diagram for Rule 18.
The solutions for these equations can be obtained in a way which emphasizes the triangular nature of the coefficient matrix:
b=(0*1)(000*1+01)* d=b.1((01+000*1)0*1)* h=d.1 g=d.(01+000*1)0* f=d.000* e=d.0 a=b.000*+0* c=b.0
The coefficients of b and d can be simplified slightly. The new
coefficient 
means that (reading from left to right)
after meeting the first 1, we can remain on the highest level only if
1's do not come in joined pairs. Having met the first such pair, we may
now remain on the second level as long as the sequence 
repeats itself, which it will do unless three 1's come along in
sequence, or else a pair of pairs enclosing a single isolated 1.
Descent to level three ensues, finally leaving a sequence without an
ancestor. Thus three ones in sequence is a sure mark of a Garden of
Eden sequence, but the other condition is much less specific, as it
does not refer to some sequence of fixed length.