Continuing the listing of de Bruijn diagrams by looking at cycle diagramscycle diagram doesn't turn up much beyond what is already in Wuensche and Lesser's Atlas [8]; in fact after increasing the arrays in LCAU they now cover the same range.
Table 3: Number of configurations of given cycle and period.
The x's in Table 3 mark unavailable periods, but the limit to the lengths of periods increases exponentially leaving little point to trying to incorporate this detail into the table. Equally, there is an exponential limit to the lengths of prime cycles running across columns, to be noted alongside the fact that multiples of periods are periods.
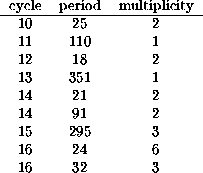
Table 4: Long periods up to cycle length 16.
Amongst these first sixteen cycle lengths are some which have periods too long for inclusion in Table 3; they are listed in Table 4.
But in both the de Bruijn diagrams and the basin diagrams there is an interesting item of note, the short height of the basin of attraction for the quiescent state (0, that is), which doesn't pass 9 and is frequently shorter.
The basin diagram for zeroes is cummulative, since anything which evolves to zero stays zero. But since a line of ones is the only alternative, it is interesting to see what produces ones for each ring circumference. That is where the small height is noticeable.
Table 5: summary of the structure of the de Bruijn diagrams for evolution to
the constant value 0.
Note that cycles of length 10 seem to be favored. That also shows up in the de Bruijn diagrams for evolution to the constant value 1:
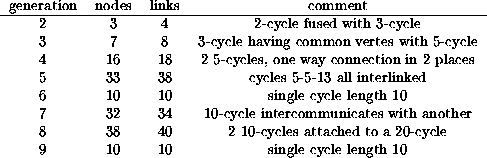
Table 6: summary of the structure of the de Bruijn diagrams for evolution to
the constant value 1.