![]()
Un sistema se dice reversible si en cada etapa del mismo uno puede conocer y ser capaz de regresar a la etapa anterior, este concepto tiene aplicaciones inmediatas dentro de la computación ya sea en la creación de sistemas encriptadores de datos o en la codificación de información para su almacenado en dispositivos físicos.
Un ACL se dice reversible si para cada configuración global existe un único ancestro capaz de generarla; en realidad podemos decir que por si misma la regla de evolución nunca define un mapeo local reversible pues siempre existe un desequilibrio entre el número total de vecindades posibles y el número de estados del ACL, es decir, en la regla de evolución de un ACL(k,r) existen k^(2r +1) vecindades diferentes que generan k estados, sin embargo este mapeo puede ser tal que induzca un mapeo global el cual si pueda ser reversible.
El punto interesante al hablar de ACL reversibles es que la regla de evolución del mismo, que es de influencia local, genera un comportamiento global del sistema el cual tiene la cualidad de preservar la información del mismo sin disiparla, por lo que un estado global en el tiempo t sólo tiene un único estado global ancestro en el tiempo t-1 y a su vez es el único que pueda evolucionar en el estado global del tiempo t+1, sin importar el tamaño que tenga el anillo de células del estado global.
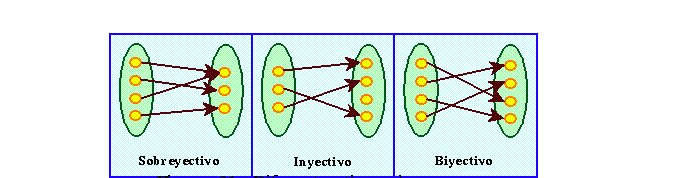
Figure 31: Diferentes tipos de mapeos.
Dado que estamos hablando de mapeos, podemos decir que un ACL reversible define un mapeo global que es sobreyectivo dado que cada estado global tiene al menos un ancestro y a la vez es inyectivo pues cada estado global tiene a lo más un ancestro; es decir se define un mapeo global biyectivo entre estados globales.
![]()