![]()
Los trabajos de [2] y [7] definen que un ACL es sobreyectivo si cada posible cadena de estados tiene un número de ancestros igual a k^(2r ) (Teorema de Multiplicidad Uniforme).
Tomemos el siguiente ACL(4,h) regla 7E186F90.
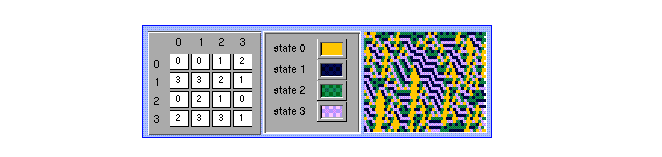
Figure 32: ACL(4,h) regla 7E186F90.
Como se puede observar en la matriz de evolución cada estado aparece el mismo número de veces que el resto, siendo este número igual a k^(2r ) o al número de nodos en el diagrama de de Bruijn; formemos ahora los ancestros de las cadenas 0, 01, 013 y 0132.
La figura ilustra que estas cadenas tienen el mismo número de ancestros cada una, lo que continua sucediendo no importa cuanto crezca la cadena en longitud (Teorema 5.2 en [2]); si ésto sucede para toda cadena posible de estados, entonces se define un mapeo global sobreyectivo, es decir, el autómata carece de Jardín del Edén.
Para saber que el número de ancestros es igual a k^(2r ) o al número de nodos en el diagrama de de Bruijn, tomemos del ejemplo anterior los ancestros de la cadena 01, utilizemos éstos para formar nuevas cadenas que evolucionan en una secuencia constituida por los estados 01X01 en donde X es el conjunto de secuencias de estados de tamaño 2r.
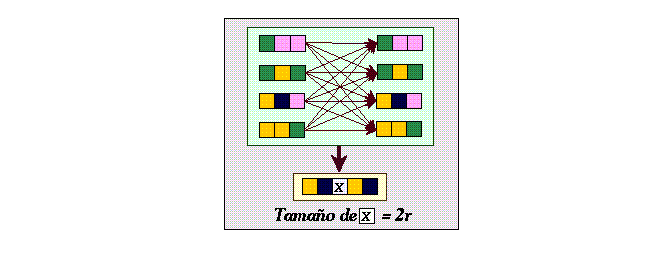
Figure 33: Ancestros de la cadenas 01X01.
Si el número de ancestros es a, entonces la nueva cadena 01X01 tendrá a2 de posibles antecesores; ahora bien, como se mostró anteriormente toda secuencia en un mapeo sobreyectivo tiene a posibles ancestros lo que también ocurre para cada posible secuencia
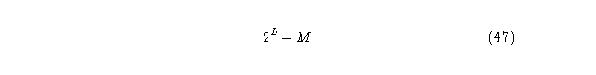
y debido a que existen k^(2r ) diferentes tipos de esta secuencia, tenemos que del mismo modo el número de posibles ancestros de la secuencia 01X01 está dado por ak^(2r ).
Al final obtenemos que a2 = ak^(2r ) ó que a = k^(2r ), es decir, que el número de ancestros de cada posible cadena de estados es igual a k^(2r ) ó al número de nodos en el diagrama de de Bruijn (Teorema 5.3 en [2]).
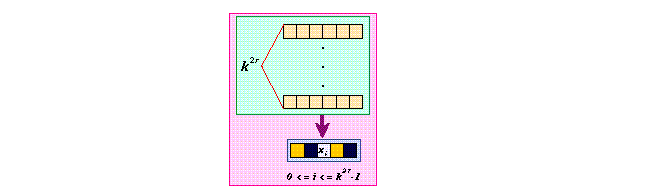
Figure 34: Los ancestros de cada posible cadena de estados es igual a
k^(2r ).
Ahora definamos 3 índices multiplicativos para describir como se conforma esta multiplicidad, estos son R, M y L (sección 14 en [2]); ejemplifiquemos ésto con un autómata (4,h) regla B46363B4.
El índice R enumera el máximo de extensiones que se le pueden hacer a una cadena a la derecha las cuales evolucionen en la misma secuencia.
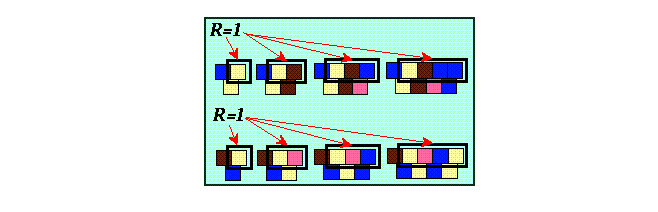
Figure 35: Ejemplo del índice R en el autómata (4,h) regla B46363B4.
El índice L cuantifica el máximo de extensiones hacia la izquierda que puede tener una secuencia y tengan la misma evolución.
Por último M señala cual es el mínimo de secuencias a las que se les puede hacer dichas extensiones por ambos lados para evolucionar en una misma cadena.
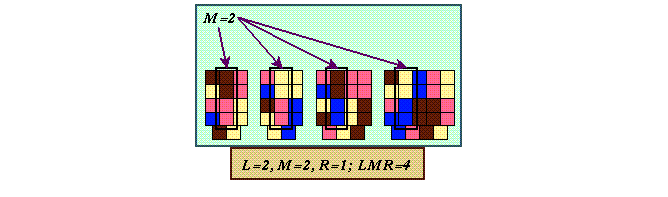
Figure 36: Ejemplo del índice M en el autómata (4,h) regla
B46363B4.
Si estos valores cumplen que el resultado de su producto es igual a k^(2r ), se define entonces un mapeo global sobreyectivo inducido por la regla de evolución; una forma en que se puede conocer cuales son los valores de L y R es haciendo uso de las matrices de conectividad de cada estado que se obtienen del diagrama de de Bruijn, en donde la suma de valores de cada renglón muestra el número de extensiones compatibles empezando desde la célula representada por el renglón i con
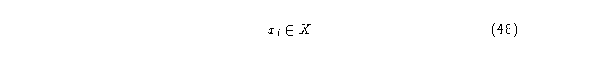
y la suma de valores de cada columna enumera las extensiones compatibles por la izquierda terminando en la célula representada por la columna j con
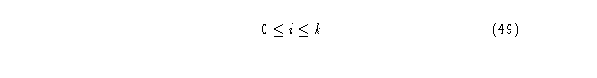
Sin embargo, las matrices de conectividad solo nos muestran por sí solas cuales son los diferentes ancestros para las cadenas de longitud 1, dado que los valores de L y R se pueden presentar en cadenas de mayor longitud, debemos buscar un proceso el cual nos permita leer estos índices para dichas secuencias, ésto se logra haciendo la multiplicación de las matrices de conectividad consigo mismas para así obtener los posibles ancestros para cadenas de longitud mayor que 1; utilizemos para ejemplificar ésto un ACL(4,h) regla BF6A15C0.
Podemos observar que por sí solas las matrices de conectividad definen valores de R=3 y L=1 teniendo que R*L=3 que no es igual a k^(2r ) o a algún submúltiplo del mismo con el cual se pueda deducir un valor de M tal que LMR = k^(2r ); sin embargo, haciendo algunas de las posibles multiplicaciones de matrices obtenemos otras nuevas matrices de conectividad para secuencias de estados mayores que 1 como las siguientes:
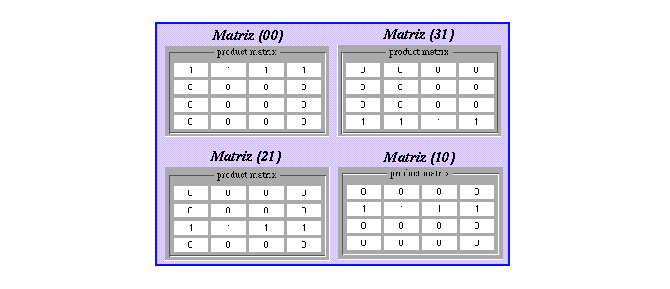
Figure 37: Multiplicación de las matrices de conectividad del autómata
(4,h) regla BF6A15C0.
Aquí las matrices definen el valor de R=4 y el de L=1; ya que estas matrices conservan sus cuatro elementos en multiplicaciones sucesivas, tenemos que la multiplicidad de este autómata es 4 por lo que estas matrices definen el valor de M=1 para estas cadenas; sin embargo, en este caso encontramos matrices las cuales nunca alcanzan esta forma, por ejemplo:
Si se continua haciendo la multiplicación de las matrices de conectividad de los estados 2 y 3 alternando, encontraremos que jamás obtendremos un valor de R=4, sin embargo, debemos recordar que los índices R y L son máximos y M es un mínimo, por lo que no es necesario que todas las matrices de conectividad o sus multiplicaciones cumplan con estos valores, con que se presenten una vez cumpliendo que RML = k^(2r ) y sean máximos y mínimo respectivamente, entonces se define un mapeo global sobreyectivo.
En realidad el uso de los índices L, R y M para detectar los posibles autómatas sobreyectivos no es necesario, simplemente se puede observar las matrices de conectividad y las multiplicaciones sucesivas de las mismas, si llegado un momento estas matrices siguen conservando su suma de elementos igual a k^(2r ) entonces podemos decir que la multiplicidad uniforme se conserva y el mapeo global es sobreyectivo (es decir, carece de Jardín del Edén); si tal mapeo en realidad no es sobreyectivo, rapidamente genera cadenas con más ancestros que k^(2r ) y otras con menos que este valor, lo que se refleja en la suma de elementos de las matrices de conectividad de dichas cadenas.
No obstante, el uso de los índices es útil para detectar autómatas reversibles, el proceso se basa en encontrar los valores de L y R; si estos valores al multiplicarse producen un resultado igual a k^(2r ) para la matriz de conectividad de toda cadena de una longitud dada, se infiere que M=1 concluyendo que sólo existe una célula para la cual es posible hacer las extensiones L y R que evolucionen en una misma secuencia y por lo tanto el autómata sea reversible (Sección 5 en [7]).
Tomemos como ejemplo un autómata(4,h) regla FFA91640 y la matriz de conectividad para la secuencia 01.

Figure 38: Autómata(4.h) regla FFA91640.
En la ilustración se observa que los ancestros de esta cadena conforman índices 1 y 4 para L y R respectivamente, aunque el valor de M es 3 para esta secuencia en particular; suponiendo que este valor de M fuera el mínimo encontrado significaría que LMR no es igual a k^^(2r k(2r ); pero si extendemos la revisión de M para secuencias de mayor longitud observamos lo siguiente:
Para que las matrices de conectividad alcancen la forma establecida en donde los valores de L y R establezcan un mapeo global sobreyectivo, necesitan que sus productos cumplan ser el producto cartesiano de dos vectores, tales vectores definen los índices de Welch; por otro lado requieren también que en su diagonal principal aparezca solo un 1, ya que ésto define un único ciclo permitido para formar tal secuencia.
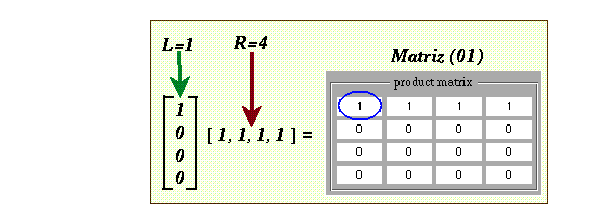
Figure 39: Matriz de conectividad como producto de un producto
cartesiano.
![]()