![]()
Podemos utilizar las herramientas gráficas que describen el comportamiento de un autómata para conocer los valores de estos índices; por medio del diagrama de subconjuntos podemos conocer los valores de R observando hasta que nivel llegan las rutas empezando desde las clases unitarias sin salir del mismo y sin que existan ciclos intermedios que impidan a las rutas llegar a este nivel.
Para conocer el índice L uno puede reflejar la regla de evolución original, es decir, trasponer el orden en que están formadas las vecindades conservando su evolución; de esta manera la nueva regla de evolución tendrá las extensiones compatibles por la izquierda de la regla original como extensiones por la derecha y de este modo el valor de L puede obtenerse directamente del diagrama de subconjuntos como se obtuvo R en la regla original, cumpliendo también que cada ruta empezando desde las clases unitarias lleguen a un nivel y no salgan del mismo, sin que existan ciclos intermedios que impidan alcanzar este nivel.

Figure 40: Valor del índice L observado en el diagrama de subconjuntos
de la regla reflejada.
Dada la naturaleza del diagrama de parejas que permite identificar secuencias originadas por varios ancestros distintos, resulta una herramienta directa para detectar cuando un autómata es reversible; si no existen ciclos más que en la diagonal principal del diagrama (que es el diagrama de de Bruijn original) entonces el mapeo global inducido por la regla de evolución es reversible.
Podemos tomar los nodos del nivel máximo a donde llegan las rutas que empiezan desde
las clases unitarias para ambos índices L y R; los nuevos diagramas que
conforman estos nodos con rutas autocontenidas se denominarán Diagramas de Welch
izquierdo o derecho respectivamente, tomemos un autómata (4,h) regla F5A0F5A0 y tomemos
sus diagramas de Welch.
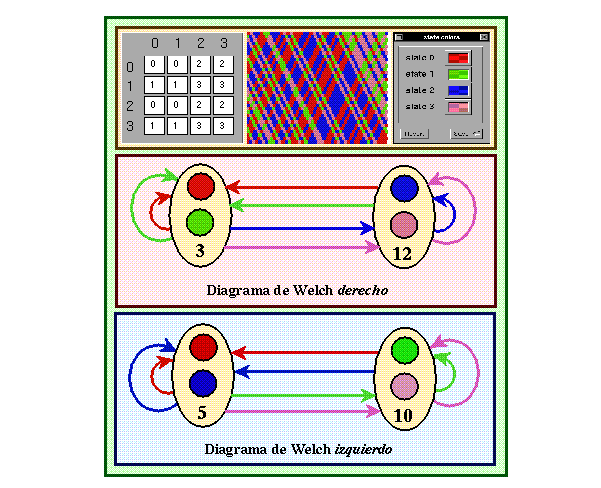
Figure 41: Diagramas de Welch del autómata (4,h) regla F5A0F5A0.
En el trabajo de [7] encontramos que un mapeo global sobreyectivo define un diagrama de de Bruijn en donde cada estado forma árboles con raíz en los ciclos, sin impedir que existan ligas sueltas, pero en el diagrama de Welch cada ruta forma un árbol con raíz en un ciclo podemos utilizar estos diagramas para obtener la regla inversa a la original; en primera la ruta con el número mayor de niveles define el tamaño de vecindad mínimo de la regla inversa, una vez que sabemos el largo de la vecindad a buscar, busquemos en el diagrama de Welch derecho cada posible secuencia del mismo largo tomando el nodo intermedio que sea común a cada ruta; por otra parte busquemos del diagrama de Welch izquierdo la misma ruta pero en orden inverso ya que este diagrama se obtuvo de la regla reflejada y guardemos también el nodo intermedio común a la misma ruta, ya que tenemos estos dos nodos tomemos el elemento en común en ambos nodos, este estado será el que defina en que evoluciona la regla inversa para dicha vecindad; por ejemplo, de los diagramas anteriores vemos que el largo máximo de cada ruta antes de caer en un ciclo es dos, de este modo tomemos todas las posibles formas para construir cada secuencia de dos estados, mostremos ésto para la secuencia de ligas 02, en el diagrama de Welch por la derecha el nodo intermedio común a cada posible modo de formar tal secuencia es 3 (estados 0 y 1); para el diagrama de Welch izquierdo formemos de todas las maneras posibles la secuencia 20, encontramos que el nodo intermedio para cada posible opción es 5 (estados 0 y 2), por último tenemos que el estado en común en ambos nodos es 0 por lo que en la regla inversa la vecindad 02 evoluciona en 0; haciendo ésto para cada secuencia posible de longitud dos se construye la regla inversa EEEE4444.
Tomando ahora el autómata (4,h) regla F5A0B5E0 se observa el siguiente comportamiento:

Figure 42: Autómata (4,h) regla F5A0B5E0 y sus diagramas de Welch.
En el diagrama derecho de Welch uno observa que la máxima longitud de cualquier ruta para que tenga un mismo nodo medio en común es 2 pero en el diagrama izquierdo esta longitud es 3; es decir, la regla inversa tiene un tamaño de vecindad igual a este valor, por ejemplo, en el diagrama derecho la ruta 02 tiene en común el nodo medio 12 mientras que en el izquierdo para la ruta 20 estos nodos son 5 y 6, esta tercia de vértices no tienen un único elemento en común y por lo tanto no se puede definir un mapeo local inverso a la vecindad 02, pero extendamos más esta secuencia tomando ahora la cadena 022, encontramos que en el diagrama derecho el nodo medio en común es 12 mientras que en el diagrama izquierdo para la cadena 220 es el nodo 5, el elemento en común entre ambos vértices es 2 y se puede establecer un mapeo local inverso para tal vecindad.
Conforme aumenta el número de estados y/o el tamaño de vecindad, por supuesto
también aumenta la complejidad de los diagramas de Welch, tomemos el ejemplo de un
autómata (6,h) regla
ZWESP7LI0ZWESP7LI0 el cual es un producto cartesiano de un
autómata (2,h) regla 10 y un autómata (3,h) regla 19305.
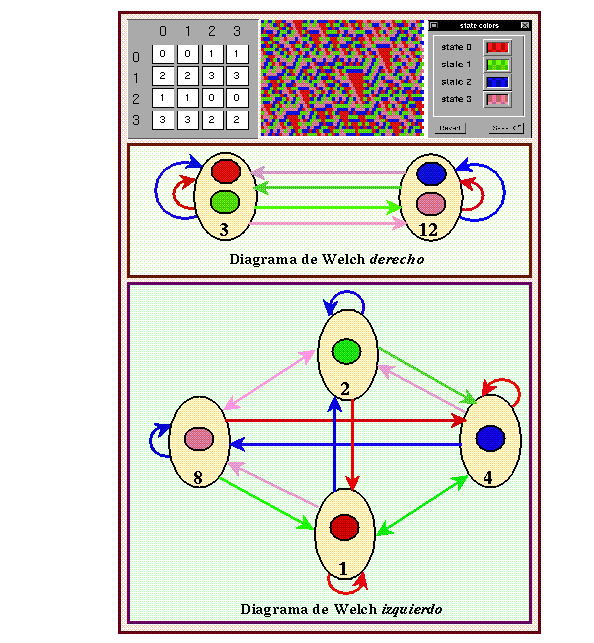
Figure 43: Autómata (4,h) regla AF05FA50 y sus diagramas de Welch.
Este autómata reversible también tiene como máximo rutas de longitud 2 en ambos diagramas, por lo que su inversa será un (6,h) también y puede ser obtenida de la misma manera que se ha explicado anteriormente.
Qué pasa con los diagramas de Welch en el caso de autómatas no reversibles, para visualizar ésto tomemos un autómata (4,h) regla AF05FA50.
Este autómata tiene un mapeo global sobreyectivo mas no reversible, es decir, carece de Jardín del Edén pero es imposible encontrar un mapeo local inverso único para una secuencia de estados dada, esto se observa claramente en los diagramas de Welch:
![]()