![]()
Los autómatas celulares han aparecido a través de la historia con diferentes nombres
(espacios celulares, estructuras celulares, arreglos iterativos), pero bajo el mismo
concepto fundamenteal. La teoría de estos autómatas, se comprende en diferentes épocas,
debidas a las aportaciones de sus principales autores. La primera comienza con John von
Neumann y la idea de las máquinas autorreproducibles; posteriormente Martin Gardner [1] publica Life, un juego para computadora planeado
por John Horton Conway y finalmente, la última etapa es comprendida por una
clasificación que proporciona Stephen Wolfram para los autómatas celulares.
Etapa de von Neumann. (1950)
A principios de los años 50's, von Neumann se preguntaba si era posible una máquina
que fuera capaz de autorreproducirse en una máquina más compleja o si habría una
contradicción lógica a esta idea, como eran tiempos de postguerra se carecía del
material para hacerla [8]. A sugerencia de Stanislaw M.
Ulam, matemático que ideaba juegos para computadora, von Neumann construyó un mode-lo
matemático abstracto, en dos dimensiones, para el análisis de la máquina, ya que de
esta forma sería más suceptible a la demostración; consistía en un tablero de damas,
donde cada casilla podría estar en cualquiera de los 29 estados diferentes definidos por
von Neumann. El estado de cada célula de la siguiente generación, dependía de los
cuatro estados más cercanos de las células vecinas en forma ortogonal.

Figure 1: Vecindad de von Neumann
El juego iniciaba con un patrón inicial y la regla determinaría todas las
configu-raciones siguientes. Von Neumann probó que la máquina autorreproducible era
posible en un mundo lógico e imaginario. El resultado fue publicado en 1966, como Teoría
de Autómatas Autorreproducibles. Posteriormente, el teorema de Edward F. Moore del Jardín
del Edén, que demostraba que si había configuraciones que no tuvieran ancestros,
entonces habría otras que tendrían múltiples ancestros. Por último el trabajo
abstracto de Hedlund con algunos resultados de la lógica simbólica, aplicables a los
autómatas.
Etapa de Gardner. (1970)
El éxito que tuvo la publicación de Life en los 70's, un fantástico juego
ecológico de computadora, inventado por Conway hizo posible el conocimiento público de
los autómatas [4]. Life, es un autómata en dos
dimensiones, donde cada célula puede tomar uno de cada dos estados, activo o quieto,
y su evolución siguiente depende de su propio estado y el de sus ocho estados vecinos, en
forma ortogonal y diagonal. Esta es la vecindad de Moore.
El criterio de Conway era que la regla no causara ninguna de las dos consecuencias
siguientes, morir rápidamente o expandirse sin límite.
Las computadoras comenzaron a tener gran popularidad y muchos programadores pusieron
interés en el juego de Conway; los dispositivos de las computadoras permitían desplegar
en forma visual las evoluciones e inclusive algunas fueron interactivas. La falta de
computadoras no fue obstáculo para los que carecían de ellas, ya que con lápiz y papel
llegaron a obtener resultados significantes.
Etapa de Wolfram. (1984)
En los estudios experimentales con autómatas, se han encontrado comportamientos
complejos en estructuras cíclicas y en estructuras muy largas [4].
La evolución de los autómatas, con condiciones iniciales aleatorias, parecen ser tan
diferentes unas con otras; sin embargo al observarlas con detalle parecen tener un
comportamiento característico en forma general.
En 1984, aparecieron tres artículos referidos a una nueva investigación en los
autómatas; dos de estos fueron escritos por Wolfram y el otro hacia referencia a él. En
los que exponía el estudio de un gran número de autómatas, que le permitió
clasificarlos dentro de cuatro clases, después de comparar sus historias evolutivas con
muchas reglas. Esta clasificación muestra que muchos detalles de la construcción de los
autómatas, son irrelevantes respecto a su conducta cualitativa.
La clasificación hecha por Wolfram [11] es la
siguiente:
Clase I. Autómatas que evolucionan rápidamente a un estado único
homogéneo.
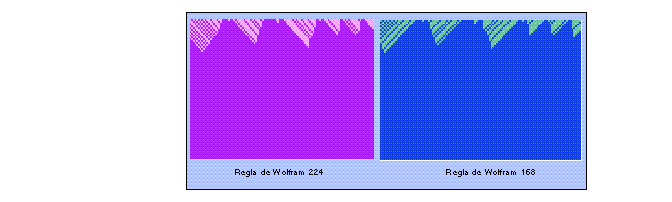
Figure 3: Para cualquier condición inicial, esta clase evoluciona en
pocas generaciones a un estado uniforme.
Clase II. Autómatas que evolucionan en estructuras cíclicas simples de
periodos cortos.

Figure 4: Alcanzan algún estado y todo lo que queda son estados
cíclicos aislados.
Clase III. Autómatas que evolucionan en conductas caóticas y estructuras
caóticas.
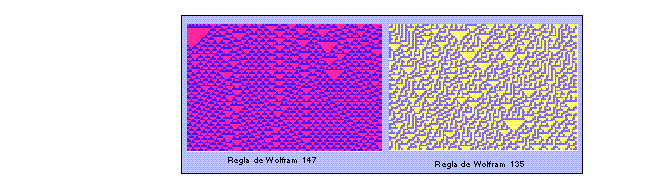
Figure 5: Más de la mitad de las reglas de Wolfram muestran este
comportamiento.
Clase IV. Autómatas que evolucionan en conductas complejas aisladas.

Figure 6: Esta es la clase más estudiada, es generada por reglas en las
cuales el diagrama de de Bruijn contiene ciertos ciclos.
![]()