![]()
Los Autómatas Celulares son sistemas dinámicos discretos, que evolucionan por
reglas determinísticas y sus variables cambian en forma sincrónica, en función de sus
valores actuales. Las palabras claves para describir a los autómatas son, discreto,
determinístico, local y sincrónico. Los autómatas lineales son versiones en
una dimensión de los autómatas de Conway. Aunque son el caso más simple, actualmente
son los más investigados, su ventaja es que su evolución puede ser representada en una
pantalla de computadora dos dimensiones, el arreglo estará limitado por el número de
pixeles de la pantalla.
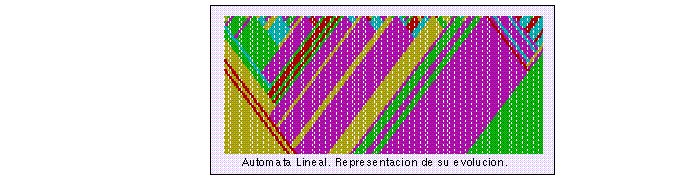
Figure 7: El autómata sigue siendo unidimensional.(No debe pensarse que
es en dos dimensiones,el t-ésimo renglón representa la configuración del autómata en
el tiempo t.)
Estos autómatas consisten en un espacio de configuración discreto de células
conectadas, cada célula tiene asignado un valor de un conjunto finito de estados y una
regla de evolución que actualiza los valores en pasos de tiempo discreto, a partir de una
condición inicial. En general los autómatas se denotan como (k,r), donde k
representa el número de estados y r, el número de vecinos [4].
Arreglos. Es el espacio de configuración discreto de células conectadas, que
puede estar delimitado o no de la siguiente forma [10]:
Doblemente infinito. El arreglo es infinito por ambos lados.
![]()
Medianamente infinito. El arreglo es infinito por alguno de sus lados.


Finito. El arreglo es finito por ambos lados.

Cuando un arreglo es finito podemos cerrarlo en forma de anillo para completar la
vecindad de sus extremos del arreglo.
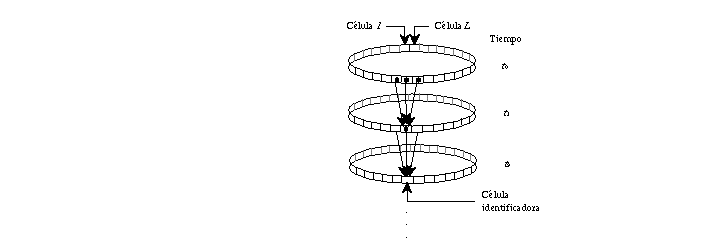
Figure 8: Este autómata es llamado cilíndrico, ya que su evolución
puede ser vista como un cilindro.
Vecinos. Todas las células de una generación se actualizan al mismo tiempo,
para cada célula, su valor en el siguiente paso del tiempo, dependerá de su propio valor
y del de las r células más cercanas, (vecinos), es decir un bloque de r
vecinos por cada lado.
El número de vecinos puede variar, lo más conveniente es tomar el mismo número de
vecinos para ambos lados de la célula, sin tomar vecindades irregulares, sin embargo esto
no siempre es posible, como veremos en los casos de los autómatas (k,h), (k,t).

Figure 9: Autómatas con diversos radios de vecindad
Estados. Los estados son los diferentes valores que puede tomar cada
célula en un autómata. El caso más simple es el binario, (sólo dos estados).
Generalmente son representados por números o colores.
Vecindad. En general, al número total de células, formado por la célula y sus
vecinos por ambos lados se le llama vecindad, y está dado por 2r+1, (donde
el producto 2r representa los r vecinos de cada uno de los dos lados). Para
todo autómata (k,r), el número total de vecindades diferentes es k^(2r+1)
No siempre el número de vecinos r es entero, en algunas ocaciones podemos tomar cada medio vecino de cada lado, (k,h), (donde h significa 1/2), para cada vecino de la célula no podemos tomar mitad y mitad, entonces es conveniente unir las dos mitades y completar un vecino de un solo lado, que puede ser el del lado derecho o del izquierdo, y la célula de la siguiente generación será puesta en el centro de sus dos ancestros. Para el caso (k,t), (donde t significa 3/2), el procedimiento es el mismo.
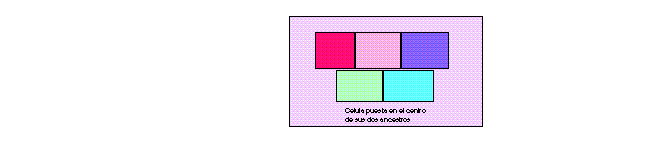
Figure 10: Ejemplo de una vecindad fraccionaria
Reglas de Evolución. La Regla de Evolución en un autómata es una
función que especifica a que estado evolucinará cada vecindad.
Existen dos maneras diferentes de formar las reglas de evolución.
Si tomamos el caso más simple de los autómatas, los (2,1), sabemos que son
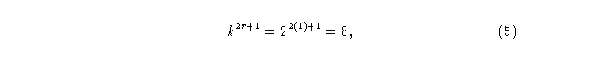
posibles combinaciones de vecindades, se ordenan de mayor a menor tomándose como
números binarios, en un segundo renglón se coloca cada estado al que evoluciona una
vecindad, si este es convertido a decimal empezando por la derecha, se encuentra la Regla
de Wolfram [4].
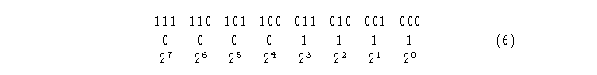
Esta es la regla 15, leyendo el segundo renglón al revés, se encuentra en número
binario 11110000.
A partir de estas vecindades se puede saber el número total de Reglas de Wolfram
que hay; ya que cada vecindad puede evolucionar en uno de dos estados hay 28 = 256
diferentes. Estas reglas son numeradas del 0 a la 255.

Existe otra forma de determinar reglas evolutivas que son llamadas Reglas
Determinísticas, son formadas por el resultado de alguna operación, (como la suma,
resta) con cada una de las vecindades. Estas reglas producen resultados muy extraños.
Supóngase la siguiente regla:
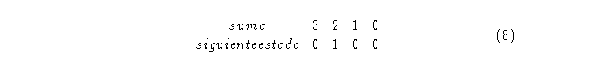
esta regla, se conforma por la suma binaria de las vecindades para saber el siguiente estado evolutivo. Esta regla también es una Regla de Wolfram, es la regla 22. Algunas otras reglas que cumplen esto son la 0, 1, 127, 150, 255.

Figure 11: Regla de Wolfram 22
![]()