![]()
Para cualquier autómata (k,h), en donde h significa que tiene vecindad
de radio igual a un medio, la fracción de vecindad para cada nodo será de una célula,
ya que 2r = 2(1/2) = 1.
Para el autómata (2,h) se tendrán dos estados:
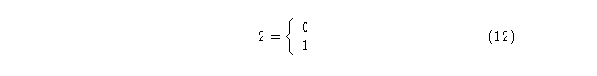
vecindad de radio igual a un medio.
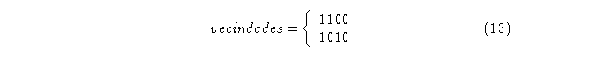
Independientemente de la tregla de evolución, el diagrama de de Bruijn estará
definido por:
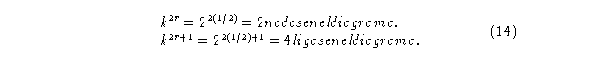
Y como se había mencionado se tendrá una fracción de vecindad de una célula.
Entonces la gráfica está dada por:

Figure 13: Diagrama de de Bruijn asociado a un autómata (2,h)
Para el autómata (3,h) se tendrán tres estados,
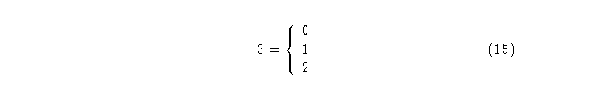
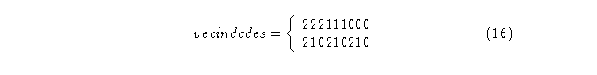
El Diagrama de de Bruijn tendrá:

Y el diagrama queda como sigue:
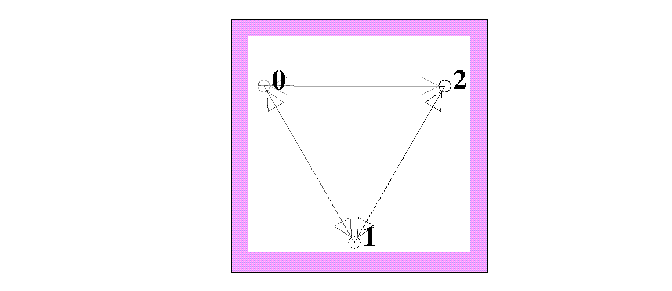
Figure 14: Diagrama genérico de de Bruijn para un autómata (3,h).
Para el autómata (4,h) se tienen 4 estados:
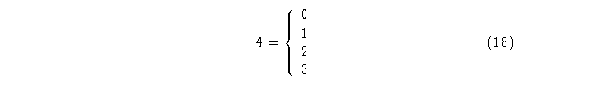
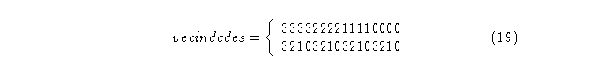
El Diagrama de de Bruijn tendrá:
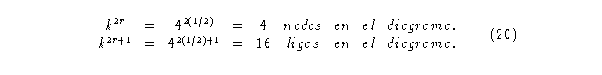
El diagrama de de Bruijn queda como sigue:
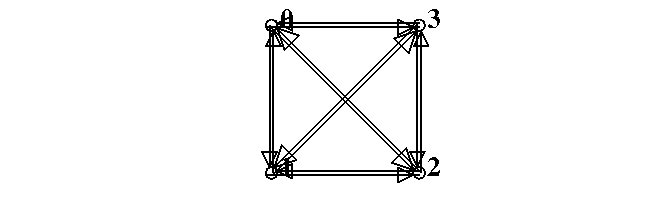
Figure 15: Diagrama genérico de de Bruijn para un autómata (4,h).
Podríamos seguir aumentando el número de estados y la complejidad del diagrama aumentaría por lo que sólo mencionaremos el autómata (8,h), que tiene 8 nodos y 64 ligas como se muestra en la siguiente figura:
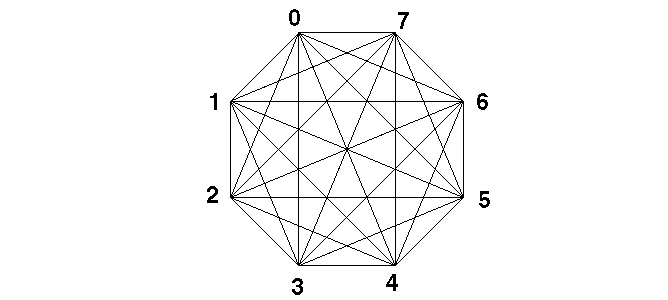
Figure 16: Diagrama genérico de de Bruijn para un autómata (8,h).
Para cualquier autómata (k,1), o sea que tiene una vecindad de radio uno, la
fracción de vecindad para el diagrama será de dos células, ya que 2r = 2(1) = 2.
Para el autómata (2,1) se tendrán:
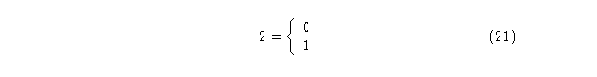
y radio de vecindad igual a uno.
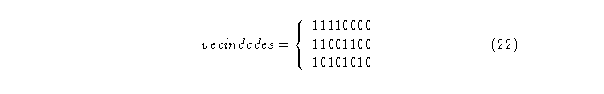
Igualmente no importa la regla de evolución, el diagrama tendrá:

Entonces las fracciones de vecindad quedan determinadas por
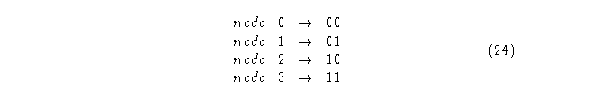
Para el autómata (3,1) se tendrán:
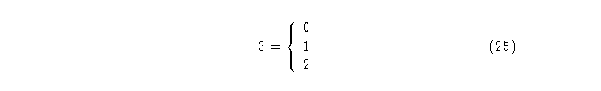
y radio de vecindad igual a uno.
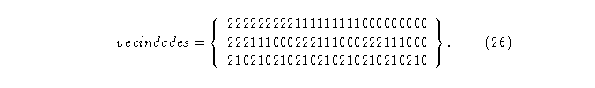
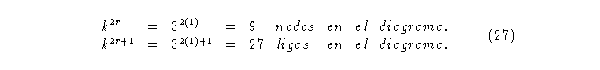
Entonces las fracciones de vecindad quedan determinadas por
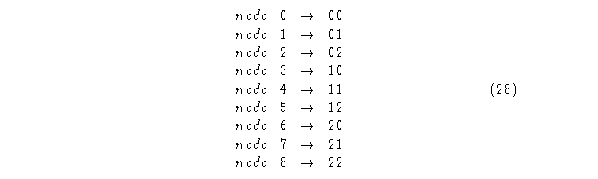
El diagrama de de Bruijn queda como sigue:
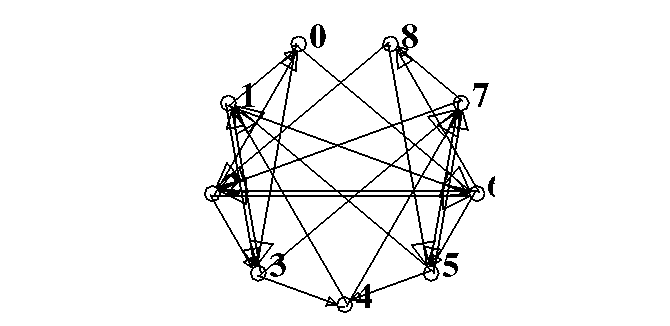
Figure 17: Diagrama genérico de de Bruijn para un autómata (3,1).
![]()