En la primera parte de éste reporte veremos que dos investigadores franceses, H. Chaté y P. Manneville presentaron en 1991 los resultados que obtuvieron numéricamente al experimentar con autómatas celulares de dimensión 
. El fenómeno que encontraron es contrario a lo que se esperaría observar según la ley de los grandes números; a este fenómeno lo llamaron comportamiento colectivo no trivial.
Se han encontrado comportamientos colectivos de naturaleza similar en autómatas celulares y en redes de transformaciones acopladas, y por lo tanto, Chaté y Manneville dieron igual tratamiento a ambos [1].
En los autómatas celulares el espacio de estados es discreto, en este caso sólo utilizaremos dos estados: el 0 y el 1. La forma en que el autómata evoluciona está definida por una regla, que es una función que especifica a qué estado evolucionará cada célula, dependiendo de la configuración de la vecindad. En redes de transformaciones acopladas, el espacio de estados es continuo, y la regla de evolución es una función real de variable real: 
es el estado de la célula i en el tiempo t.
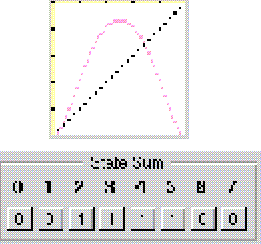
Figura 1: Curva de una aproximación de campo promedio, con la estructura de ``Life''. Regla 60 en el autómata (2,3).
En este caso se eligieron reglas de evolución totalísticas, i.e., aquellas en que se toma en cuenta el valor de sus células; así se forma un número binario que luego es convertido en un número decimal que designa a la regla totalística. Se eligieron también vecindades grandes donde cada célula tiene igual número de vecinos en todas direcciones (vecindades isotrópicas); así, la probabilidad de que una célula pase del estado 
, al estado 1 depende sólo de la suma de 1's que tiene dicha célula. Esta probabilidad de transición 
puede ser:
Los autómatas celulares estudiados por Chaté y Manneville originalmente fueron diseñados para investigar la validez de la aproximación de campo promedio, la cual busca la probabilidad de que un estado aparezca en la siguiente generación.
Las reglas de evolución consideradas tienen una estructura semejante al juego ``Life'' [6], ya que si todas las células de la vecindad son 0's se evoluciona en un 0, y si son todas 1's también se transforman en un 0.
El tipo de vecindades que consideraron para sus investigaciones son von Neumann (en 
y Moore (en d= 2), y la vecindad centro-cúbica en d= 3.
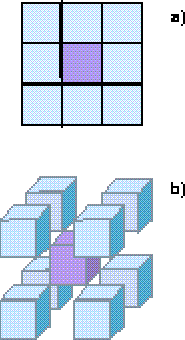
Figura 2: a) Vecindad de Moore en d= 2; b) vecindad centro-cúbica en d= 3
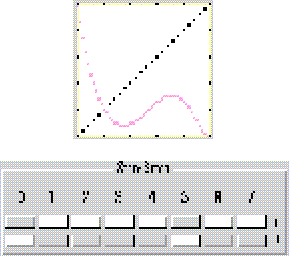
Figura 3: Curva de una aproximación de campo promedio, con la estructura propuesta por Hemmingsson. Regla 33 en el autómata (2,3).
En la segunda parte del reporte analizaremos la explicación que da J. Hemmingsson al fenómeno de Chaté y Manneville. Para Hemmingsson no se trata de un comportamiento colectivo, sino global, debido a la existencia de membranas que impiden la sincronización del comportamiento de todas las células del autómata celular.
Además, Chaté y Manneville mencionan ciertos ingredientes que creen esenciales para que sea posible observar un comportamiento pseudo-periódico, por ejemplo, que la dimensión debe ser 
, sin embargo, en 1992 Hemmingsson publicó resultados diferentes. Él encontró una regla para un autómata celular en d= 1 que presentaba un comportamiento con período 3. Lo interesante es que esta regla no tiene la estructura de ``Life'', que es otro ingrediente importante para Chaté y Manneville.
También en la segunda parte se expondrán los argumentos de Binder, quien en 1995 publicó que el comportamiento pseudo-periódico no se debe a la presencia de membranas y macrocélulas en el autómata celular.
Finalmente, en la tercera parte del reporte están las conclusiones de éste análisis de los resultados de los investigadores mencionados.
Ascelli Z. Vissuet