El comportamiento colectivo no trivial

 
Figura 4: a) Clase 1 de Wolfram, regla 251 en el autómata (2,1); b) Clase 2 de Wolfram, regla 15 en (2,1); c) Clase 3 de Wolfram, regla 120 en (2,3); d) Clase 4 de Wolfram, regla 200 en (2,3).

Al decir ``comportamiento'' nos referimos a la manera en que evoluciona el autómata a través de las generaciones en el tiempo, este comportamiento se puede apreciar al graficar mediante puntos la densidad del autómata en el tiempo t (mapa de retorno). ``Colectivo'' se refiere a cantidades que dependen de todos los elementos o células del autómata, tal como la densidad o promedio de células en el estado 1. Un comportamiento colectivo no trivial ocurre cuando se observan varias densidades en la evolución del autómata celular.

La evolución de los autómatas celulares estudiados tiene analogía con la clasificación hecha por Wolfram [6], que se comentará a continuación.

 
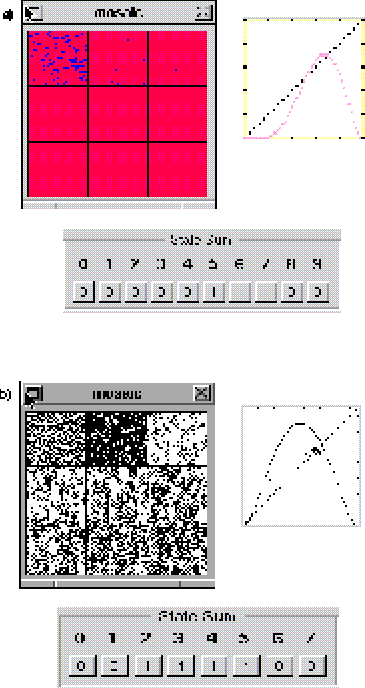
Figura 5: a) Comportamiento localmente periódico con baja concentración final. Regla 224 en (2,4), vecindad de Moore en d= 2; b) Comportamiento localmente periódico con alta concentración final. Regla 60 en (2,3), vecindad de von Neumann en d= 3. En ambos casos se muestra el plano con las primeras 9 generaciones, y el mapa de retorno.

En las familias de reglas estudiadas, a partir de una configuración inicial aleatoria del autómata celular, con una densidad inicial de células 1, se pueden observar 2 tipos de comportamiento: [1]

1. Comportamiento localmente periódico, para densidades muy grandes o muy pequeñas.
   • Con baja concentración final. La concentración inicial es muy alta, y rápidamente se llega a unas cuantas células en estado 1 en un mar de 0's, es decir, la concentración final es muy pequeña o nula. Este tipo de evolución tiene parecido con la clase 4 de Wolfram, ya que el autómata pasa por un estado transitorio largo, para finalmente quedar en algunas pequeñas estructuras periódicas.
     

   • Con alta concentración final. La concentración inicial es muy baja. Permanecen ``vivas'' (i.e., en el estado 1) más del 50 % de las células. Tiene parecido con la clase 2 de Wolfram, pues quedan estados transitorios cortos, ciclos periódicos cortos y pequeñas estructuras periódicas.
     

2. Comportamiento colectivo no trivial. Se puede observar cuando el tamaño del autómata crece, es decir, cuando el número de células es muy grande. La evolución local de una célula o de un pequeño grupo de ellas tiene muchos cambios impredecibles en la densidad global del autómata celular ruido estadístico, i.e., dicha densidad llega a patrones caóticos. Por eso se podría decir que se parece a la clase 3 de Wolfram. Sin embargo, no se llega a un caos global (el caos global se da cuando a través de las evoluciones se encuentra que hay más de un valor para describir la densidad global del autómata). La densidad global no siempre es única, pueden ser varios puntos o nubes de puntos [1].
   

   El teorema del límite central dice que ``la media muestral es asintóticamente normal con varianza '', esto significa que la distribución de probabilidad de las n medias que se pueden obtener de una población se puede aproximar por medio de una distribución normal estándar, si n es grande [7]. (A la distribución normal también se le denomina distribución de Gauss o gaussiana).
   

   De acuerdo con el teorema del límite central podemos decir que para un número grande n de células la estimación de la densidad de células ``vivas'' tiene una desviación estándar [6]. En otras palabras, el anillo o las nubes que se forman con los puntos en el mapa de retorno se definen mejor cuando crece el tamaño del autómata.
   

 
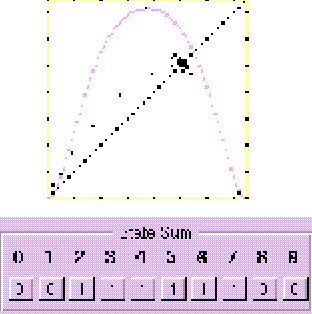
Figura 6: Comportamiento colectivo con período 1. Mapa de retorno de la regla 252 en el autómata (2,4), vecindad de von Neumann en d= 4.

De acuerdo con Chaté y Manneville, hay ciertos ingredientes esenciales para que ocurra un comportamiento colectivo no trivial [1]:

• La actualización sincronizada de todas las células es muy importante. ``Sincronizada'' significa que todas las células del autómata evolucionan al mismo tiempo en cada una de las iteraciones. Para lograr la sincronización, es necesario que en todo el autómata haya comunicación instantánea. Al iterar asíncronamente el comportamiento de cada célula o grupo de células reflejará el comportamiento de todo el autómata: un comportamiento trivial, de período igual a 1 (P1).
• Es necesaria la dimensión . A partir de d= 4 este tipo de comportamiento se hace frecuente. La dimensión debe ser finita para poder observar en el mapa de retorno la aproximación de campo promedio.
• La evolución local debe ser del tipo de ``Life'', aunque no es necesaria una evolución local específica.
• Que el autómata celular sea determinístico, en vez de probabilístico, no es indispensable.

Si las estimaciones de la densidad de células ``vivas'' siguen una distribución gaussiana [7], entonces la densidad en la configuración del autómata celular obedece a la ley de los grandes números [6]. Esto quiere decir que si la distribución de probabilidad de la media muestral tiene una varianza que disminuye conforme crece el número n de células, entonces la estimación de la media poblacional será muy cercana a su valor real, cuando n sea muy grande. Y por lo tanto, estaremos haciendo un buen cálculo de la densidad de células 1 del autómata.

La ley de los grandes números nos dice que la media muestral converge en probabilidad a la media poblacional cuando el tamaño n de la muestra crece:

para cualquier número positivo . Es por esto que en muchas investigaciones se obtiene el promedio de las mediciones, esperando obtener una mayor precisión en la estimación de la media poblacional [7].

 
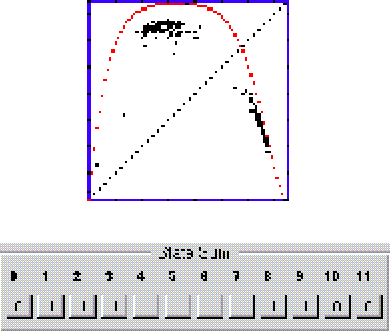
Figura 7: Comportamiento colectivo con período 2. Mapa de retorno de la regla 1022 en (2,5), vecindad de von Neumann en d= 5.

En el caso de autómatas celulares y de redes de transformaciones acopladas, al crecer el número de células con que se experimenta, se esperaría obtener un buen estimador de la densidad global (análoga a la media poblacional). Lo sorprendente es que en estas simulaciones se obtuvieron comportamientos periódicos y pseudo-periódicos en los que no hay una única densidad, sino varias. Esto es precisamente lo que caracteriza a un comportamiento no trivial. Cuando se presenta un comportamiento colectivo no trivial con período 3 en el mapa de retorno, se observan 3 nubes de puntos, es decir, 3 densidades diferentes. En el caso de pseudo-período 3, los vértices del toro triangular también indican 3 densidades. El interior de éste anillo o toro suele quedar vacío, es decir, la evolución del autómata no tiende a una densidad única, como se esperaría en base a la ley de los grandes números.

 
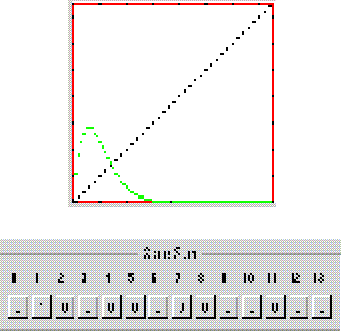
Figura 8: Chaté y Manneville reportan un comportamiento colectivo con período 4 en la regla 2 en el autómata (2,6), vecindad de von Neumann en d= 6. En la figura no se observa, tal vez por ser diferente el número de células empleadas.

 
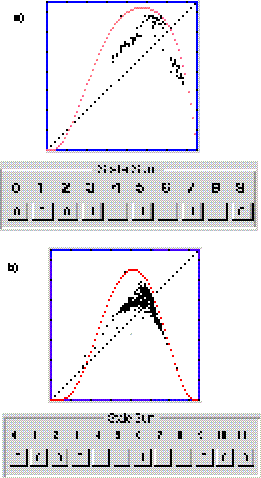
Figura 9: Mapa de retorno que muestra comportamiento colectivo. a) Período 3, regla 504 en (2,4), vecindad de von Neumann en d= 4; b) Pseudo-período 3, regla 496 en (2,5), vecindad de von Neumann en d= 5.

En un comportamiento colectivo no trivial la evolución local puede llegar a presentar casi cualquier configuración, es decir, es caótica; por lo tanto hay al menos un exponente de Lyapunov positivo (un número que indica el grado de caos local) [1]. ``Los exponentes de Lyapunov miden la tasa de transmisión de información dentro de un autómata celular, y son un límite superior para la entropía, la cual mide el contenido de información de los patrones generados al evolucionar el autómata. La existencia de exponentes de Lyapunov positivos es una característica importante de los autómatas celulares de clase 3 ''[6].

Otra forma de medir el caos es ver al autómata como un conjunto de subsistemas con cierta correlación entre sí. El caos global del autómata debe crecer con el número de subsistemas, y por lo tanto, debería ser proporcional al número de células que forman el autómata. En un autómata celular caótico la densidad de células ``vivas'' no se estabiliza alrededor de uno o algunos valores, sino que toma muchos valores distintos.

No se originan cambios significativos en el comportamiento global de redes de transformaciones acopladas o de autómatas celulares cuando se hacen pequeñas modificaciones de la regla de evolución local, por eso se puede decir que el comportamiento colectivo no trivial es robusto. Basta con que d sea suficientemente grande para poder observar un comportamiento de este tipo.

La mayoría de las reglas de autómatas celulares son robustas, pues su comportamiento se mantiene ante pequeños cambios hechos a dicha regla.

• Clasificación de los resultados