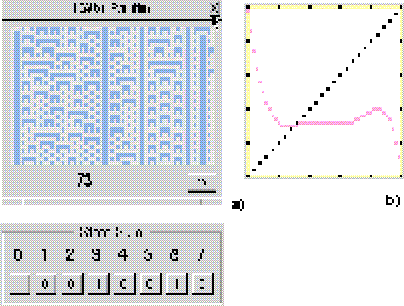
Figura 13: Regla 73 en el autómata (2,1), vecindad de von Neumann en d= 1. a) Evolución que presenta membranas; b) Mapa de retorno.
La investigación de Hemmingsson se enfoca a cómo partes separadas del autómata tienen acceso a la misma información. Esta división en subsistemas o macrocélulas es debida a las paredes de Bloch que se forman. Estas paredes o membranas están ubicadas aleatoriamente en el autómata celular, se conservan a través de las generaciones, tienen densidad finita, y entre 2 paredes adyacentes hay un número finito de células. Cada conjunto de células es una macrocélula aislada del resto, y dentro de ellas se dan ciclos o períodos. Las paredes no desaparecerán ni permitirán interacción alguna entre las macrocélulas. [4].

Figura 13: Regla 73 en el autómata (2,1), vecindad de von Neumann en d= 1. a) Evolución que presenta membranas; b) Mapa de retorno.
Para d= 1 y d= 2 es fácil encontrar las paredes de Bloch, sin embargo, para ![]() se hace difícil definirlas. Por eso Hemmingsson dice que en d= 3 no hay paredes de Bloch, pero que en su lugar hay una estructura ``de cebolla'', es decir, diferentes capas que tienen células con el mismo número de vecinos 1. Cuando dichas capas interactúan (aunque hay poca interacción), el resultado es un comportamiento pseudo-periódico [4].
A causa de que hay poca interacción o acoplamiento, no parece adecuado describir a este tipo de autómatas como redes de transformaciones acopladas [2], contradiciendo así a Chaté y a Manneville. Éstos investigadores consideraron que se observaban comportamientos colectivos de naturaleza similar en los autómatas y en las redes de transformaciones acopladas, y dieron igual tratamiento a ambos [1].
se hace difícil definirlas. Por eso Hemmingsson dice que en d= 3 no hay paredes de Bloch, pero que en su lugar hay una estructura ``de cebolla'', es decir, diferentes capas que tienen células con el mismo número de vecinos 1. Cuando dichas capas interactúan (aunque hay poca interacción), el resultado es un comportamiento pseudo-periódico [4].
A causa de que hay poca interacción o acoplamiento, no parece adecuado describir a este tipo de autómatas como redes de transformaciones acopladas [2], contradiciendo así a Chaté y a Manneville. Éstos investigadores consideraron que se observaban comportamientos colectivos de naturaleza similar en los autómatas y en las redes de transformaciones acopladas, y dieron igual tratamiento a ambos [1].
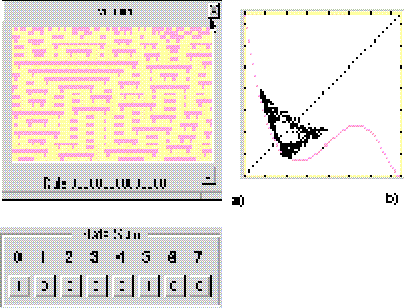
Figura 14: Regla 33 en el autómata (2,3), vecindad de von Neumann en d= 3. a) Evolución que presenta membranas; b) Mapa de retorno que presenta un comportamiento colectivo no trivial de pseudo-período 3, en forma de anillo triangular.
Una explicación para la interacción de éstas macrocélulas sería una influencia externa sobre todo el autómata, pero en tal caso, el intercambio de información no sería lo suficientemente rápido [2]. La explicación que Hemmingsson apoya es que una configuración inicial homogénea (por medio de un generador de números aleatorios) le da a todas las macrocélulas que forman el autómata la misma información inicial, y entonces ya no será necesaria la comunicación entre dichas macrocélulas. Por lo tanto, la sincronización global se debe al estado inicial del autómata [2] [4]. Entre más grande sea el número de células, se hace más predecible la evolución del autómata, ya que para calcular la densidad global se obtiene una media sobre todas las macrocélulas [2].
Para Hemmingsson la evidencia de una sincronización global no justifica la sincronización en la evolución del autómata celular. Comenta que tal vez no sea necesaria la sincronización en la evolución para poder observar un comportamiento colectivo periódico o pseudo-periódico, y que por lo tanto, el comportamiento global observado por Chaté y Manneville no es un fenómeno colectivo [2].
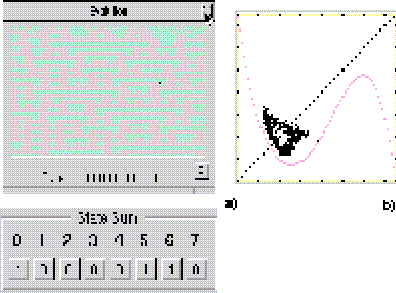
Figura 15: Regla 97 en el autómata (2,3), vecindad de von Neumann en d= 3. a) Evolución que presenta membranas; b) Mapa de retorno que presenta un comportamiento colectivo no trivial de pseudo-período 3, en forma de anillo triangular.
En autómatas celulares de 1 dimensión, Hemmingsson experimentó con la regla 73 (que tiene una estructura diferente a ``Life'') y su conjugada, la regla 109, en una vecindad de tamaño 3. En este autómata celular se encontraron paredes de Bloch. Iniciando con una configuración aleatoria, el autómata celular pasó por un estado transitorio y finalmente presentó un comportamiento con período tres [4], aunque Chaté y Manneville no lograron observar su fenómeno en d= 1. Por lo tanto, Hemmingsson encontró que la regla 73 en d= 1 tiene algunas propiedades de un autómata celular de dimensión mayor [2]. Cabe aclarar que en d= 1 la periodicidad observada es local (a nivel de vecindades o de regiones localizadas), porque a nivel global, la densidad del autómata tiende a período 1.
En dimensión d= 3 Hemmingsson experimentó con la regla 33 (que también tiene una estructura diferente a ``Life'') y su regla complemento, la regla 123, en una vecindad de von Neumann, con una configuración aleatoria y densidad de células ``vivas'' de 0.5, en un autómata de ![]() células. Hemmingsson dice que ésta regla es la única totalística en d= 3 que tiene un comportamiento pseudo-periódico en el mapa de retorno [2] [3], tal como el fenómeno observado por Chaté y Manneville, incluso con el mismo ruido estadístico. Con la regla 33 ocurre un comportamiento no trivial cuando se comienza con una densidad pequeña de células en estado 1. Si la densidad inicial se va a los extremos, i.e., todas las células en 0 ó todas en 1, entonces el comportamiento observado sería trivial [3].
Además, Hemmingsson encontró el número promedio de revoluciones completas en cada generación [2] [3]. Este número es -0.3371, i.e., aproximadamente cada 3 generaciones el toro triangular en el mapa de retorno da una vuelta completa. El signo negativo indica que el triángulo gira en el sentido del reloj.
células. Hemmingsson dice que ésta regla es la única totalística en d= 3 que tiene un comportamiento pseudo-periódico en el mapa de retorno [2] [3], tal como el fenómeno observado por Chaté y Manneville, incluso con el mismo ruido estadístico. Con la regla 33 ocurre un comportamiento no trivial cuando se comienza con una densidad pequeña de células en estado 1. Si la densidad inicial se va a los extremos, i.e., todas las células en 0 ó todas en 1, entonces el comportamiento observado sería trivial [3].
Además, Hemmingsson encontró el número promedio de revoluciones completas en cada generación [2] [3]. Este número es -0.3371, i.e., aproximadamente cada 3 generaciones el toro triangular en el mapa de retorno da una vuelta completa. El signo negativo indica que el triángulo gira en el sentido del reloj.
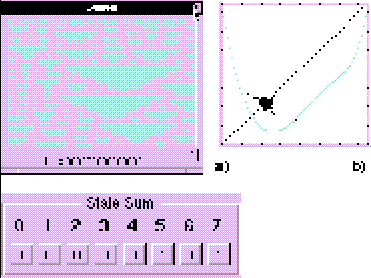
Figura 16: Regla 161 en el autómata (2,3), vecindad de von Neumann en d= 3. a) Evolución; b) Mapa de retorno que presenta un comportamiento colectivo no trivial de pseudo-período 3, en forma de anillo triangular.
Cabe mencionar que Hemmingsson no hace comentarios respecto al resto de las reglas. Simplemente dice con cuáles trabajó y los resultados que obtuvo. Y tal vez está omitiendo algunas reglas que también presentan el comportamiento colectivo de período 3 ó de pseudo-período 3. Por ejemplo, H.V. McIntosh ha encontrado otras reglas totalísticas en d= 3 con la estructura de la regla 33 de Hemmingsson que muestran el efecto de Chaté y Manneville: en la regla 97 ocurre un comportamiento colectivo no trivial pseudo-periódico. Y en d= 4, encontró la regla 129, en cuya evolución se observa un comportamiento de período 3. En la regla 161, aunque la curva del mapa de retorno no tiene la misma estructura, se observó un pseudo-período en d= 3.
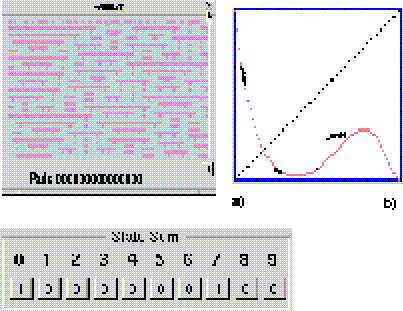
Figura 17: Regla 129 en el autómata (2,4), vecindad de von Neumann en d= 4. a) Evolución; b) Mapa de retorno que presenta un comportamiento colectivo no trivial de período 3, en forma de tres nubes de puntos.
Ascelli Z. Vissuet