Estos comportamientos colectivos se identifican rapidamente de manera muy general en sus diagramas de evoluciones para diferentes concentraciones 
iniciales.
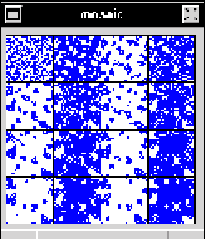
Figura 5: Periódo dos, regla 61 AC(2,4)
Como podemos observar en la Figura 5, el diagrama de evoluciones para la regla totalística 61 muestra comportamientos periódicos de tamaño dos, en cuatro dimensiones empleando la vecindad de von Neumann. Este análisis lo podemos extender con el mapa de retorno y verificar que la existencia de los puntos fijos, es la que determina ésta periodicidad.
Podemos gráficar un mapa de retorno, calculando las densidades 
a través del tiempo donde,
y de esta manera podemos determinar la existencia de las acumulaciones de varios puntos en uno o varios puntos fijos. Donde las nubes que produce dicha gráfica, nos ilustran el número de periódos del autómata celular; facilmente comprobable a través del diagrama de evoluciones.
En todos los casos estamos tomando diferentes valores de 
, distribuidos uniformemente un 
en toda la lattice. Aunque iniciemos con configuraciones aleatorias, el resultado es el mismo.
Finalmete obtenemos como resultado de la equación 2, la promedia por la cantidad de 1's que existen dentro de la lattice en el tiempo t. Iterando esta lattice en el tiempo t+1, t+2, 
y así sucesivamente para varias t's, determinado por el valor que tome N. Y está acumulación de varios puntos, nos indican los puntos fijos de la función determinada por mean field.
Figura 6: Diagrama de retorno, regla 61
Mean Field Theory nos indica la probabilidad de obtener 1's en la siguiente generación, esta función podemos obtenerla graficando el polinomio derivado de la regla totalística. Iluatramos este procedimiento con la regla totalística 61, tenemos que las vecindades 3, 5 y 7 evolucionan en 1. De esta manera las vecindades determinan los coeficientes del polinomio, que calculamos con el triángulo de Pascal, y finalmente tenemos:
donde q = 1-p, como podemos comprobar en la Figura 7.
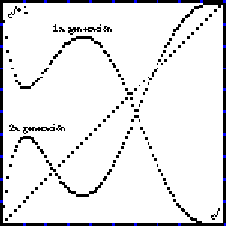
Figura 7: Diagrama de mean field, regla 61
Producimos un mapa iterativo f dada una concentración de 1's, dentro de la lattice y calculamos la probabilidad de obtener unos en la siguiente generación, entonces tenemos:
si las reglas son totalísticas,
Con la aproximación del campo medio, la probabilidad para una vecindad 
de tener exactamente S unos, es representado como una binomial:
finalmente tenemos que las reglas que tienen la misma 
, 
y 
tienen la misma aproximación y su mapeo es determinado como:
Por ejemplo si tenemos un autómata celular (2,3), d=3, 
y definimos una regla totalística 60 (
notación de Chaté-Manneville) donde el intervalo 2(
)-5(
), nos indica que las vecindades 
, 
, 
y 
mapean a uno y las cuatro vecindades restantes mapean a cero. Y damos una densidad inicial 
, entonces tenemos en la siguiente generación:
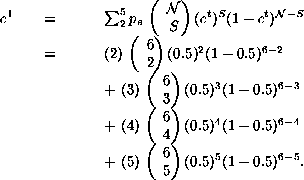
y así a través del tiempo. Podemos notar que conforme aumenta la dimensión del autómata celular en estudio, el grado del polinomio crece drasticamente por el número de vecindades que se generan. Siendo un buen problema tratar de resolver polinomios de grado 11 o más.
Dados estos resultados, podemos notar que la aproximación que realizamos a través de mean field es muy buena, a lo contrario que afirman Chaté-Manneville. Esto ha sido comprobado con los descubrimientos de Hemmingsson [8], encontrando comportamientos colectivos en autómatas de menor dimensión.
Presentamos uan pequeña lista de autómatas celulares con comportamientos periódicos de orden k=2, r=3 y r=4 en la Tabla 1.
