Figura 8: AC(2,3), regla 33, d=3

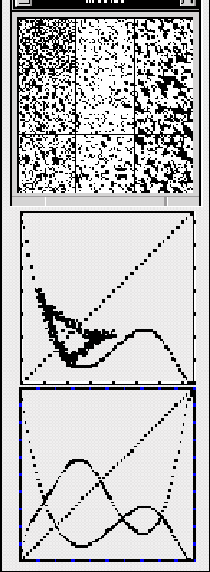
Figura 8: AC(2,3), regla 33, d=3
El comportamiento quasiperiódico es un comportamiento periódico que no está bien definido. Dado este comportamiento, podemos notar rapidamente en el diagrama de retorno que los puntos fijos no estan bien definidos, pues todos los puntos de acumulación oscilan entre los puntos fijos.
La Figura 8 muestra comportamientos quasiperiódicos de longitud 3, para el autómata celular (2,3) regla 33 y d=3 dimensiones.
Podemos ver perfectamente en el diagrama de transiciones, como los puntos de acumulación a través del tiempo oscilan alrededor de un triángulo limitado por tres puntos fijos en sus extremos. En el diagrama de evoluciones podemos verificar estos resultados, la evolución de toda la lattice a través del tiempo es claramente quasiperiódica.
Finalmente calculamos mean field para la primera y la segunda iteración, está última es una reflexión de la primera curva, podemos verificar que la curva se intersecta en tres puntos con la segunda generación. Si calculamos las siguientes probabilidades para la tercera generación y la cuarta generación, podemos verificar que la curva de probabilidad para la cuarta generación es muy parecida a la curva de probabilidad de la primera generación. Por lo que mean field aproxima de manera muy cercana y precisa el comportamiento del autómata celular a través del tiempo.
Presentamos varios ejemplos ilustrativos de comportamientos periódicos y quasiperiódicos para varios autómatas del tipo (2,3) y (2,4).
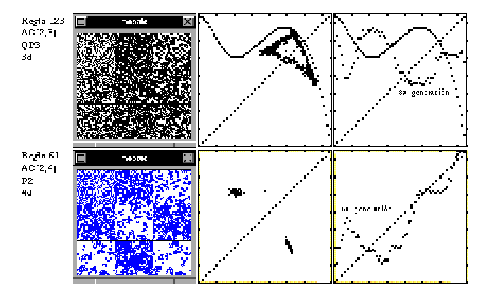
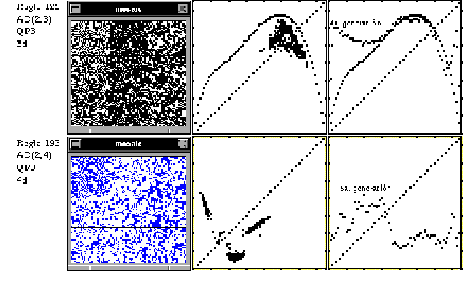
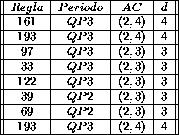
Tabla 2: Autómatas periódicos y quasiperiódicos