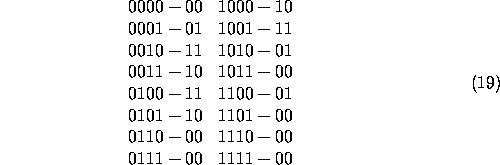
En un autómata (2,1) necesitamos un bloque de tamaño 4 que al evolucionar se convierta en un bloque de tamaño 2.
A continuación se muestran todos los posibles bloques de 4 células (ancestros) así como sus hijos (cadenas resultantes) después de aplicarles la regla 22.
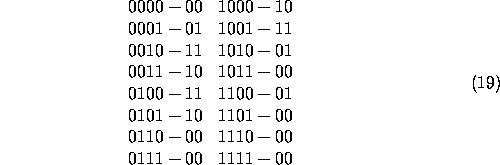
Ahora el problema se transforma en el cálculo de una cadena de dos elementos. Suponga que deseamos calcular la probabilidad de que aparezca la cadena 01 (en realidad puede ser cualquier cadena como mas tarde veremos, ya que nuestro objetivo final es el cálculo de una la aparición del estado 1, es decir una cadena cuyo elemento es 1).
Para llevar a cabo este cálculo se tiene que
![]()
Es decir, la probabilidad de que aparezca una cadena es igual a la suma de la probabilidad de que se den sus ancestros.
Sabemos que la probabilidad de que aparezca 0001 es:
![]()
que la probabilidad de que se de la cadena 1010 es:
![]()
y finalmente la probabilidad de que se aparezca la cadena 1100 es:
![]()
Por lo tanto, la probabilidad de que se de la cadena 01 estara definida por:
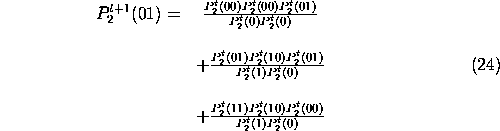
o
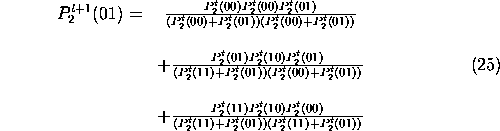
donde por las condiciones de Kolmogorov podemos expresar la probabilidad de que aparezca 01 en términos homogéneos, es decir, en términos de cálculos de bloques de 2 células, ya que:
![]()
Como se puede apreciar de esta ecuacuón para calcular la probabilidad de que aparezca la cadena 01, se tiene que calcular la probabilidad de las cadenas 00, 10 y 11. O en otras palabras las probabilidades de que aparezcan todas los ancestros de las cadenas de dos elementos: las cadenas de cuatro elementos.
Siguiendo pasos similares a los del cálculo de la probabilidad de 01, se tiene que la probabilidad de que aparezca 00, 01 y 11. Entonces la solución del cálculo de la probabilidad de 01 esta dado por el siguiente sistema de ecuaciones:

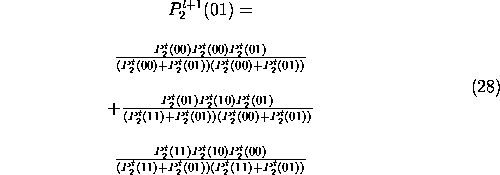
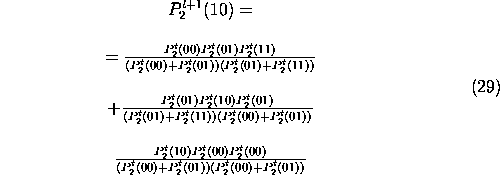
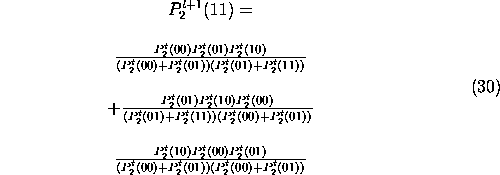
Resolviendo este sistema de ecuaciones tendremos la probabilidad para todas las posibles cadenas de dos estados, es decir las cadenas 00,01,10 y 11. Pero lo que buscamos nosotros es la probabilidad de aparición del estado 1, una vez más por Kolmogorov, tenemos que sumando dos de nuestros anteriores resultados, en particular
![]()
tendremos la probabilidad de que aparezca el estado uno.
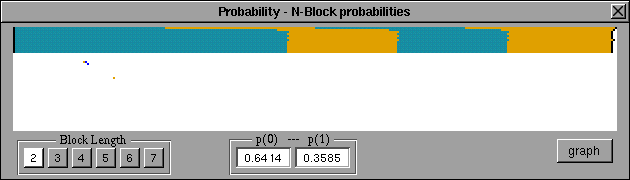
Figura 3: Gráfica de la probabilidad de un bloque de tamaño 2
En el paquete NXLCAU podemos encontrar también la opción N-Block, que realiza la gráfica de la probabilidad de bloques de tamaño n. En dicha gráfica, cada barra es uno de los bloques de tamaño n que se pueden formar; y el ancho de cada uno depende del número de bloques de tamaño (n+2r) que transforman en un bloque de tamanõ n.
En la figura 3 mostramos dicha gráfica. Por ejemplo en la gráfica 3 la primera columna representa las transformaciones al bloque (00), la segunda al bloque (01), la tercera al bloque (10) y por último al bloque (11). Dado que la regla 22 transforma en su mayoría a 0, la columna mas ancha es la primera.