Un autómata celular 
es un sistema dinámico determinista con espacio, tiempo y estados discretos, el espacio se divide en N celdas, cada una contendrá uno de los k estados, generalmente estarán en el rango de 0 a k-1, y un radio r. Su función para la i-ésima celda esta dada por:
Por simplicidad trabajaremos con un autómata celular (2,1).
La densidad es la probabilidad de escoger una celda al azar en algún momento en particular durante la evolución del autómata y encontrarlo en el estado 1.
La concentración en el tiempo t esta dada por:
donde M es el tamaño de la red y 
el estado de la i-ésima celda asignando valores de 0 y 1.
Teoría del campo medio es una aproximación que usa las reglas del autómata, el cual nos indica la concentración 
apartir de una concentración 
. Gráficamente la concentración 
será el eje de las X y 
será el eje de las Y, existen otro tipo de gáficas como las series de tiempo, en donde el tiempo será el eje de las X y las concentraciones el eje de las Y.
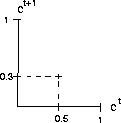
Figura 1: Explicación gráfica de la teoría de campo medio. Dada una densidad 
en el tiempo t obtenemos una densidad 
en el tiempo t+1
La simulación de Monte Carlo al igual que la teoría del campo medio nos indica la concentración 
a partir de una concentración 
. Su diferencia con la teoría del campo medio es que Monte Carlo ocupa los datos reales, por lo que es posible calcular su aproximación en cualquier generación. La gráfica resultante se puede comparar con la de teoría del campo medio.