En este caso tomaremos un autómata celular con dos estados y un vecino por cada lado,
es decir un autómata 
. La regla se representa de
dos formas ya sea en notación binaria o en notación decimal. En este caso se tienen ocho
vecindades de tamaño tres.
Figura 2.3: Regla de evolución del autómata (2,1) regla 30.
Consecuentemente k=2 y s=2, tenemos 
nodos y 
ligas, que a su vez se
pueden identificar los nodos como el número de estados del autómata y las ligas el
número de vecindades del autómata. Los estados estan formados por las fracciones de
vecindad: 00, 01, 10 y 11, que en notación decimal se representan como los estados: 0, 1,
2 y 3. Como se había mencionado en la sección anterior la naturaleza de los estados no
es muy importante si no más bien la regla de evolución que afectan a las vecindades.
Para mayor ilustración los estados se representarán a través de colores. La función de
transición 
, indica el mapeo de la vecindad en el
tiempo t al nuevo estado de evolución en el tiempo t+1.
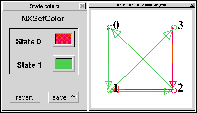
Figura 2.4: Diagrama de de Bruijn para la regla 30.
Para obtener el diagrama de subconjuntos emplearemos la tabla de relaciones de la
Sección 2.3, entonces tenemos 
nodos en el
diagrama de subconjuntos, que son exactamente todos los subconjuntos que se formaron en
esa misma sección, ahora bien estos subconjuntos se representaran en notación decimal
como se ilustra en el siguiente cuadro:
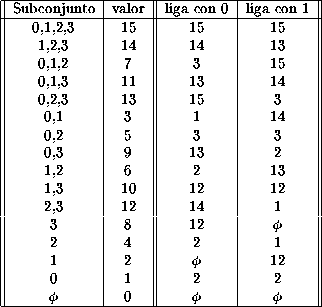
Tabla 2.2: Conectando subconjuntos.
en este cuadro podemos observar perfectamente las cuatro clases unitarias que existen dentro del diagrama empezando por el conjunto máximo hasta llegar al conjunto mínimo, las columnas tres y cuatro muestran a que subconjunto se liga el subconjunto de la primera columna y con que estado. De esta manera se obtienen todas las ligas en el diagrama de subconjuntos.
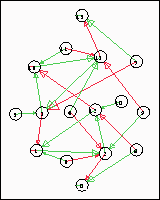
Figura 2.5: Diagrama de subconjuntos para la regla 30.
Para construir el diagrama de parejas efectuaremos el producto carteseano de las
matrices de conectividad del diagrama de de Bruijn. En este caso tendremos 
parejas ordenadas que a su vez son el número de nodos
del diagrama de parejas. Esta matriz recibe el nombre de la matriz T y sus
subíndices estan formados por todas las parejas posibles 
, donde a y b pertenecen a 
,
es claro notar que los subíndices de la primera submatriz son las parejas ordenadas (0,0), (0,1), (0,2) y (0,3). Como ejemplo, el subíndice (0,0) contiene un ciclo consigo mismo ya que el estado cero evoluciona en el mismo cero y así para toda la matriz. A continuación se mostrara el diagrama de parejas completo, cabe señalar que de este diagrama se pueden producir dos diagramas más, uno de ellos puede ser el diagrama ordenado donde la simetría mostrada en el diagrama original se pierde y el otro diagrama es el que nos muestra exclusivamente los ciclos que se forman a través de ciertas secuencias dadas. Para estos diagramas los ciclos autocontenidos se representan como un radio dentro del nodo.
Figura 2.6: Diagrama de parejas para la regla 30.