Sea 
, 
y f es una función.
Entonces si 
decimos que f
mapea a a sobre b y denotamos esto como 
. Por lo tanto denotamos un mapeo f del
conjunto A al conjunto B por 
. El término mapeo se usa como un sinónimo de función [17].
El mapeo de los estados dentro del diagrama de evoluciones puede ser representado en un diagrama de Venn, como conjuntos. Donde el conjunto A representa las configuraciones posibles y el conjunto B los estados de evolución.
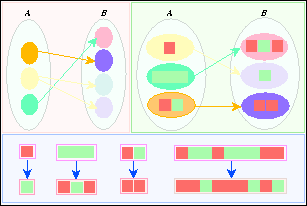
Figura 3.1: Mapeo de estados representado como conjuntos.
En la Figura 3.1 el primer diagrama de Venn ilustra el mapeo entre conjuntos de elementos no definidos, partiendo de este punto de referencia podemos representar estos elementos como configuraciones de tamaño n, mapeando sobre estados que pudiesen ser sus estados de evolución en el siguiente paso. Posteriormente presentamos diferentes tamaños de configuraciones mapeando a sus respectivos estados de evolución en la siguiente generación.
Nótese la poca importancia que se les a dado a k y a r; esto es por razones de informalidad pues el objetivo de los diagramas es sólo identificar el mapeo de las mismas configuraciones en los diagramas de evoluciones. Posteriormente se especificarán en detalle estos tipos de mapeo de tamaño variado.
El primer detalle que vamos a tratar, es el mapeo no simétrico dentro del diagrama de
evoluciones. El caso que más se ha estudiado hasta estos momentos es el autómata (2,1),
es decir, dos estados y un vecino por cada lado, pero recordemos que el número de estados
puede crecer tal como (3,1), (4,1), (5,1), (6,1), ... , y el radio de vecindad también
(2,2), (2,3), (2,4), ... . Pero tenemos autómatas tales como 
, 
, 
,
... , donde 
, 
, 
y así sucesivamente.
Ilustrando para el caso más trivial el autómata 
, la h nos indica medio vecino por cada
lado, pero en lugar de tomar medio vecino por cada lado se toma uno completo ya sea a la
izquierda o a la derecha y de esta forma conservamos la simetría dentro del diagrama de
evoluciones.
Figura 3.2: Mapeo para el caso r=h.
Una vez identificado como se comporta el mapeo en los autómatas celulares se analizaran los diferentes tipos de mapeos que pueden originarse, estos tipos de mapeos son muy importantes para poder analizar el comportamiento del autómata y obtener una buena clasificación de los mismos mapeos.