El mapeo local [16] determina el comportamiento de los autómatas celulares dentro del diagrama de evoluciones en localidades específicas. Estas propiedades las podemos ver en el mismo diagrama de de Bruijn, donde la función de transición determina el mapeo local para cada una de las vecindades existentes en un estado dado. Ahora formalizaremos estos conceptos para tener una idea más clara del mapeo local.
Sea 
un conjunto no
vacio de símbolos llamado alfabeto o estados. La cardinalidad de 
se denota como 
. Una secuencia de longitud finita de símbolos en
es llamada una cadena
sobre 
. El conjunto de
todas las cadenas sobre 
es
denotado por 
. Si 
es el conjunto de todas las
cadenas de longitud n sobre 
. Sea c una configuración sobre 
. El conjunto de todas las configuraciones sobre 
es denotado por 
. El conjunto de todas las
configuraciones finitas sobre 
es denotado por 
.
Sea 
, 
y el mapeo 
, entonces 
es llamado un mapeo local de k- símbolos
de n- longitud si 
, para 
. Si
esto es verdadero, entonces el conjunto de todos los mapeos locales de k-símbolos
de n-longitud es denotado por 
, por lo que 
.
Masakasu Nasu desarrolla el mapeo local finito y no finito de un modo general y
abstracto. Para comprender esta simbología analizaremos un autómata celular (2,1) con k=2
y r=1. Si 
es el
conjunto del alfabeto o estados, entonces el conjunto de 
para el autómata (2,1) esta representado como 
. Además k es el
número de estados dentro del autómata y el número de estados es dos por lo que k=2,
entonces la cardinalidad de 
es igual al valor de k, si esta condición se cumple entonces ahora podemos
calcular el valor de n.
Como n es la longitud de las cadenas sobre 
, este es definido como el tamaño de cada una de
las vecindades, es decir, para este autómata (2,1) n=3, ya que tenemos una célula
central y un vecino a la izquierda y otro a la derecha tal como se había definido en la
Sección 1.1, por lo tanto el tamaño de cada una de las vecindades 2r+1 es igual a
n. Consecuentemente 
denota el conjunto de todas las cadenas de longitud n, este conjunto de cadenas no
son más que las mismas vecindades que pueden llegarse a formar {(000), (001), (010),
(011), (100), (101), (110), (111)}. Para el caso del autómata (2,1) tenemos ocho
vecindades de tamaño tres, compuestas por los estados que pertenecen a 
.
Finalmente podemos determinar el mapeo local 
para el autómata (2,1) de k-símbolos y n-longitud
y una regla dada. Dado que, si tenemos ocho vecindades diferentes de tamaño tres,
entonces a cada una de ellas le corresponde un único estado de evolución o estado al que
mapea cada vecindad. Esto es la función de transición para un autómata (2,1) dada por 
donde las x
representan los estados, i la posición donde se encuentra cada estado dentro de la
lattice y t representa el tiempo (generación o iteración) de cada una de las
celulas en cierta configuración c, dentro del diagrama de evoluciones.
Sin embargo observemos la cantidad de mapeos que existen para cadenas de longitud n,
este valor puede variar considerablemente de acuerdo al número de estados y al radio de
vecindad que contenga el autómata en estudio. Por lo que la función de transición 
depende de k y r.
Si 
P 
, entonces 
es una configuración finita de longitud l,
por lo que se deduce que 
.
El mapeo local puede efectuarse tanto en configuraciones finitas 
como en configuraciones no finitas c.
Este es un punto importante, una configuración finita es un vector renglón que se
encuentra dentro de la lattice de longitud l; n puede estar ubicado dentro
de cualquier i-ésimo sitio de la configuración, sea finita o no finita. Por lo
tanto, un mapeo local puede efectuarse sobre configuraciones no finitas.
Autómata celular (2,1)
Si 
y 
. Si r = 1, entonces 2r+1 = n = 3
por lo que la función de transición para este caso es 
. Dada la regla 01111000 (30 en decimal) la
función de transición denota la siguiente tabla para mapeos locales sobre
configuraciones finitas y no finitas:
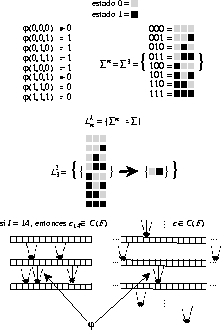
El diagrama de de Bruijn representa adecuadamente los mapeos locales para autómatas
celulares de orden 
. Para
el caso del autómata celular (2,1) regla 30 los mapeos estan dados por las aristas del
diagrama siguiente:
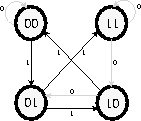
Figura 3.3: Mapeos locales para la regla 30.
Como podemos ver el mapeo local se deriva de una regla específica para un valor dado,
aún así Nasu define el conjunto 
como el conjunto de todos los mapeos locales. Esto quiere decir que si
tenemos un atómata celular (2,1) con n = 3, tendremos 
mapeos locales.
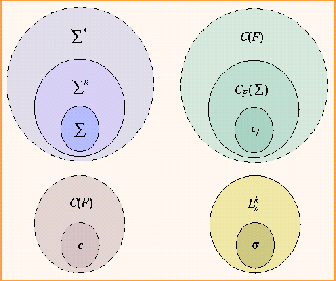
Figura 3.4: Conjuntos de estados, configuraciones y mapeos.
Genaro Juárez Martínez
E-mail:genaro@sparcomp.cs.cinvestav.mx