Un mapeo biyectivo [16] es cuando tenemos un
único ancestro. Sea A el conjunto de las configuraciones finitas 
en el tiempo t-1 y B
el conjunto de las configuraciones finitas 
en el tiempo t. Entonces definimos un mapeo biyectivo si
existe una correspondencia uno a uno y además sobre [17] del conjunto A al conjunto B.
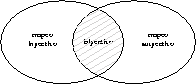
Como podemos ver en la Figura 3.15 el mapeo biyectivo implica que por cada elemento que existe en el conjunto A debe de existir un mapeo único para cada uno de los elementos del conjunto B.
El mapeo biyectivo es la intersección del mapeo inyectivo y el mapeo suryectivo [19], por lo que el mapeo biyectivo carece de configuraciones pertenecientes al Jardín del Edén y configuraciones con múltiples ancestros.
Esto quiere decir que para toda configuración 
en el tiempo t, esta configuración tiene un único
ancestro en el tiempo t-1 y un único sucesor en el tiempo t+1. El mapeo
biyectivo juega un papel muy importante dentro del estudio de los autómatas celulares reversibles,
las mismas propiedades globales que manifiestan este tipo de mapeo a sido uno de los
principales puntos de investigación [20] en los
últimos años. Es importante señalar que el mapeo biyectivo presenta propiedades muy
importantes tanto gráficas como matriciales. La determinación y representación adecuada
de los autómatas reversibles la trataremos con mayor detalle en el capítulo siguiente,
mencionando algunos algoritmos existentes para obtener tales autómatas, así como sus
propiedades elementales para una mejor identificación de los mismos.
Por último dentro del diagrama de transiciones el mapeo biyectivo se comporta de
manera cíclica como se puede observar en la Figura 3.16; su representación de acuerdo a
la definición señalada anteriormente ilustra de manera precisa este comportamiento para
cualquier configuración 
, en este caso el autómata celular en estudio es
un autómata binario regla 15. Los dos primeros diagramas de transiciones para las
configuraciones globales tienen una longitud de l = 2, en el diagrama de cuatro
nodos l = 4, en el diagrama de seis nodos l = 6, en el diagrama de ocho
nodos l = 8 y en el último diagrama de diez nodos l = 10.
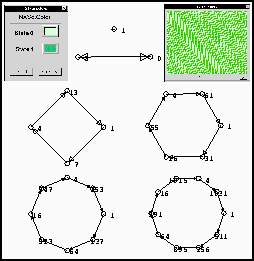
Figura 3.16: Transiciones biyectivas.
Genaro Juárez Martínez
E-mail:genaro@sparcomp.cs.cinvestav.mx
