Un mapeo suryectivo [16] es cuando tenemos al
menos un ancestro. Sea A el conjunto de las configuraciones finitas 
en el tiempo t-1 y B
el conjunto de las configuraciones finitas 
en el tiempo t. Entonces definimos un mapeo suryectivo si
existe una correspondencia sobre [17] del
conjunto A al conjunto B.
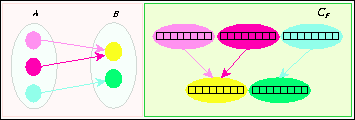
Figura 3.12: Mapeo suryectivo.
Esto quiere decir que siempre existirá al menos una imagen del conjunto A sobre
el conjunto B. Dentro del diagrama de evoluciones implica que una configuración 
tiene uno o más ancestros,
esto es podemos construir esa misma cadena a partir de una o más cadenas en el tiempo t-1.
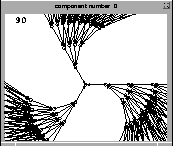
Figura 3.13: Mapeo suryectivo regla 90.
El mapeo suryectivo tiene la característica de que no existen configuraciones
pertenecientes al Jardín del Edén, esto se debe por que todas las configuraciones tienen
uno o más ancestros. Si examinamos el autómata binario regla 90 en la Figura 3.13
podemos observar dentro el árbol topológico para las configuraciones 
con l = 8 localizados en una i-ésima
posición, configuraciones 
con 
. El diagrama de
transiciones es útil para poder observar las múltiplicidades que existen sobre las
mismas transiciones. Sin embargo podemos verificar esta propiedad apartir del mismo
diagrama de de Bruijn y el diagrama de subconjuntos.
De manera informal, el diagrama de de Bruijn nos indica que un mapeo es suryectivo si
el número de ligas dado por algún elemento que pertenece a 
es igual a cada uno de los demás elementos que
pertenecen a 
para el caso
cuando r=h. Si analizamos las matrices de conectividad y el mapeo es suryectivo
entonces:
.
El diagrama de subconjuntos debe de carecer de secuencias que vayan del conjunto máximo al conjunto mínimo, esto implica que no existen configuraciones pertenecientes al Jardín del Edén. Para verificar con mayor exactitud todas estas múltiplicidades [2] [16] podemos construir el diagrama de parejas y analizar las secuencias que tienen uno o más ancestros. Regresemos al autómata binario regla 90 cuyo mapeo es un mapeo suryectivo.
Figura 3.14: Propiedades de un mapeo suryectivo.
En la Figura 3.14 tenemos que las matrices de conectividad por estado para la regla 90 cumple con la condición de que la cardinalidad de la matriz A es igual a la cardinalidad de la matriz B, esto implica que el diagrama de de Bruijn debe tener igual número de aristas del estado cero y del estado uno. El diagrama de subconjuntos nos indica que no existe ruta alguna que vaya del conjunto máximo al conjunto mínimo, además las posibles secuencias que pueden llegarse a formar no exceden de cuatro transiciones a lo más. Esto nos indica que si construimos sus respectivos árboles topológicos ellos tendran una altura máxima de cuatro transiciones y además sobre la misma clase unitaria, ya que las clases unitarias se encuentran autocontenidas en ciclos de longitud mayor igual que uno y menor igual que cuatro sin salir de estas. Finalmente el diagrama de parejas confirma el mapeo suryectivo, pues nos muestra los ciclos que se forman fuera de la diagonal lo que implica que existen secuencias de cadenas que tienen más de un posible ancestro.