![]()
Se puede identificar tres vertientes principales en donde se han utilizado AC para
algún propósito:
Dentro de este contexto se busca simular sistemas en donde el comportamiento de los mismos se rija por la interacción local de sus componentes, de este modo se han podido modelar el crecimiento de cristales, incendios forestales, modelos de reacciones químicas como la reacción de Belousov-Zhabotinsky, mecánica de fluidos, patrones de pigmentación de piel, crecimiento de conchas marinas y corales, comportamiento de colonias de microorganismos entre otros; ejemplos de estas aplicaciones se pueden encontrar en [8,24].
En este campo se utilizan a los AC para estudiar áreas como complejidad, sistemas
caóticos, termodinámica, entropía, computación en paralelo, computación universal,
teoría de lenguajes computacionales o estudio de patrones fractáles como se muestra en [12,25].
Aquí se busca construir un AC que sea capaz de desarrollar un proceso en especial, esto puede ser desde creación de fondos para diseños artísticos, procesamiento de imágenes o encriptación de datos [8]; se han creado ACL que realizan tareas muy sencillas como podría ser un ACL(2,1) que dada una configuración inicial, produzca después de un número finito de pasos un estado global fijo dependiendo que estado sea mayoritario en la configuración inicial [4].
Se puede observar que estos campos de desarrollo no son excluyentes, ya que un mismo trabajo puede caer en las tres vertientes, un ejemplo puede ser el AC de von Neumann, ya que puede ser visto como una simulación de la autorreproducción de organismos microscópicos, se puede estudiar en éste el funcionamiento de un sistema complejo y es un AC que realiza una tarea en especial, la replica de él mismo.
Mostrando un ejemplo muy sencillo de una aplicación, propongo un ACL que ordene de izquierda a derecha en orden descendente una secuencia aleatoria de ceros y unos después de un número finito de pasos.
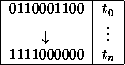
Tabla: Ordenación de una secuencia de 0's y 1's.
Para resolver esta simple tarea se tomará un ACL(3,1) donde dos estados representan los valores de 0 y 1 a ordenar y el tercero será un margen para la ordenación, la regla de evolución de tal autómata es la siguiente:

Tabla: Regla de evolución QD3QD3Q03 para un ACL(3,1).
Esta regla de evolución del ACL(3,1) se clasifica QD3QD3Q03 utilizando en ésta una notación de base 27 en bloques de 3 para este ACL en especial, la regla se lee empezando desde la vecindad 222.
Analizando un poco la regla de evolución, se observa que el estado 0 hace corrimientos a la derecha, el estado 1 a la izquierda y el estado 2 permanece estable al evolucionar, a continuación se presenta un ejemplo de su funcionamiento en donde la configuración inicial es una secuencia aleatoria de 0's y 1's, limitada a los lados con el estado 2.

Figura: Ordenación de una secuancia aleatoria de 0's y 1's con un
ACL(3,1) regla QD3QD3Q03.
En este ejemplo es posible ver de manera muy sencilla una computación en paralelo que hace el ACL propuesto al ordenar al mismo tiempo varias secuencias aleatorias de 0's y 1's.
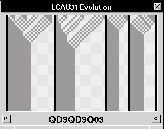
Figura: Ordenación `` paralela'' de secuancias aleatorias de 0's
y 1's con un ACL.
![]()