El diagrama de de Bruijn nos representa como evolucionan los vecindarios en un
ACL, sus orígenes vienen de la teoría del registro de corrimientos; los nodos del
diagrama representan vecindades parciales del ACL, si éste tiene k estados y un
tamaño de vecindad 2r+1 el diagrama tendrá 
vértices y 
ligas.
Los nodos resultan de tomar cadenas diferentes de tamaño 2r formadas con los k estados y las ligas unen los nodos para formar las vecindades completas donde los últimos 2r-1 elementos del nodo donde parte la liga deben concordar con los primeros 2r-1 elementos del nodo adonde llega, es decir, cuadrando como fichas de dominó y el color o etiqueta de la liga representa la evolución de la vecindad; tomemos un ACL(2,1) regla 90.
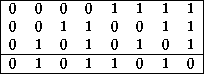
Tabla: Regla de evolución 90 de un ACL(2,1).
El diagrama de de Bruijn correspondiente tendrá 
nodos con 
ligas.
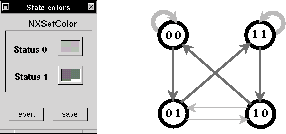
Figura: Diagrama de de Bruijn de un ACL(2,1) regla 90.
El ciclo en el nodo 
significa que la vecindad 000 evoluciona en el estado 0, la liga que va del
nodo 
al 
señala que la vecindad 001
evoluciona en 1 y así sucesivamente; para facilitar la representación gráfica se
renombran los nodos con valores enteros del 0 en adelante, así el mismo diagrama
toma la siguiente forma:
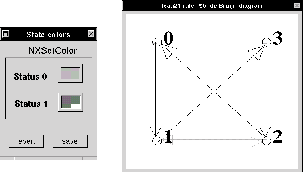
Figura: Diagrama de de Bruijn renombrado de un ACL(2,1) regla 90.
Esta gráfica también tiene una representación matricial a la cual se denomina matriz de evolución, donde los índices representan los nodos y sus elementos el valor de la liga que une del índice del renglón al de la columna.
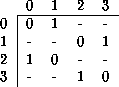
Tabla: Matriz de evolución de un ACL(2,1) regla 90.
Otro ejemplo del diagrama de de Bruijn ahora para un ACL(4,h).
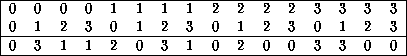
Tabla: Regla de evolución 0F08725C de un ACL(4,h).
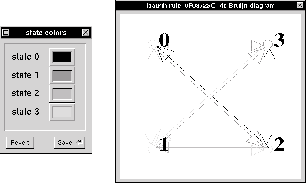
Figura: Diagrama de de Bruijn de un ACL(4,h) regla 0F08725C.
La matriz de evolución de dicho ACL(4,h) será:
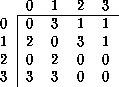
Tabla: Matriz de evolución del ACL(4,h) regla 0F08725C.
Una aplicación trivial del diagrama de de Bruijn es recobrar los valores de las células que al evolucionar producen una cadena dada de estados, por ejemplo para el ACL(4,h) la cadena 001 puede ser consecuencia de la evolución de las células 0002 ó 3203.