![]()
El producto cartesiano de dos gráficas tiene muchas aplicaciones, por ejemplo comparar rutas entre dos diagramas diferentes o dos rutas en el mismo diagrama, ésta es la función del diagrama de Parejas [14] el cual también toma como base al diagrama de de Bruijn; los nodos del diagrama de parejas son duplas de nodos del diagrama de de Bruijn, las ligas unen nodos donde ambos miembros de un nodo están conectados con la misma liga con los miembros del otro, de este modo las rutas del diagrama de parejas corresponden a parejas de rutas iguales en el diagrama de de Bruijn que por supuesto no tienen que compartir los mismos nodos, se puede decir que el diagrama original está implícito en el diagrama de parejas.
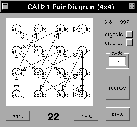
Figura: Diagrama de Parejas de un ACL(2,1) regla 22.

Tabla: Matriz del diagrama de parejas del ACL(2,1) regla 22.
Comparando esta matriz con la matriz de evolución del mismo ACL se observa que la
primera es una extensión de la segunda ya que donde aparece un cero en la matriz de
evolución se presenta la matriz de conectividad de ceros en la de parejas, es decir ésto
es el resultado del producto tensorial (elemento x matriz) de la matriz de evolución con
las matrices de conectividad por estados del diagrama de de Bruijn.