Como se vió anteriormente, se llama Jardín del Edén al conjunto de todas aquellas cadenas de estados que no puedan aparecer en la evolución del ACL más que en la configuración inicial; el diagrama de subconjuntos indica de manera muy clara cuales son estas cadenas, ésto se observa si existe una ruta que vaya desde el subconjunto de máxima cardinalidad hasta el conjunto vacio y la secuencia de arcos de tal ruta es justamente la cadena que pertenece al Jardín del Edén de dicho ACL; esta ruta nos muestra que no importa desde que estado partamos en el diagrama de de Bruijn, llegará un momento en que no se pueda encontrar una liga para completar dicha ruta (justamente la liga que nos lleva al conjunto vacio), ejemplifiquemos esto de manera sencilla con un ACL(2,1) regla 231.
Figura: ACL(2,1) regla 231 y su diagrama de subconjuntos.
En este caso se ve claramente que en el diagrama de de Bruijn uno no puede formar la
ruta 00 empezando desde cualquier nodo, esta es la misma ruta que aparece en el
diagrama de subconjuntos que va desde el nivel mas alto al conjunto vacio, y como se nota
en la evolución del autómata, las cadenas formadas por dos o más 
aparecen solo en la configuración inicial; el diagrama de
subconjuntos nos indica que configuraciones pertenecen al Jardín del Edén, es decir, si
el ACL es sobreyectivo o no, si tales rutas no existen, entonces la regla de evolución
define un mapeo global sobreyectivo.
Pero aun podemos obtener más información acerca del ACL, en especial de los índices de Welch, esto es ya que un arco que parte de un nodo a otro en el diagrama de subconjuntos está conformado por el conjunto de arcos donde al menos un estado de subconjunto inicial tiene ligas con los estados de subconjunto final.
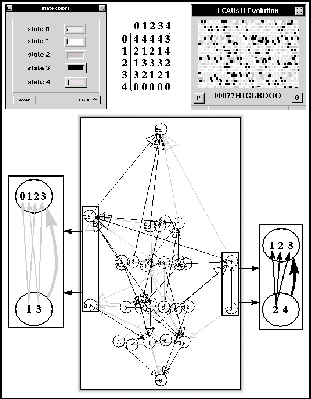
Figura: ACLR(5,h) regla 00077HIGLBDOO y su diagrama de subconjuntos.
En el diagrama de subconjuntos anterior se observa que el nodo 10 formado por los estados 1,3, tiene una liga de valor 2 con el nodo 15 formado por los estados 0,1,2,3, esta liga está constituida por las ligas que van del estado 1 del nodo 10 a los estados 0,2 del nodo 15 y las ligas del estado 3 del nodo 10 a los estados 1,3 del nodo 15; lo mismo ocurre en el caso de los nodos 20 y 14.
Si tomamos las rutas que parten desde los subconjuntos unitarios podemos conocer cual es la cardinalidad de los conjuntos compatibles por la derecha de cada estado observando a que subconjuntos llegan los arcos; si el ACL es reversible todas las rutas que empiezan desde los subconjuntos unitarios terminan en subconjuntos con cardinalidad R o en el conjunto vacio, cumpliendo así con la propiedad de combinabilidad que Nasu especifica.
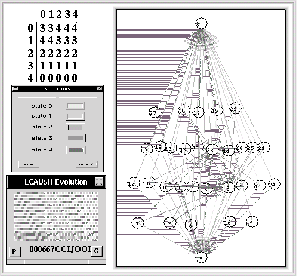
Figura: ACLR(5,h) regla 000667CCIJOOI y su diagrama de subconjuntos.
En la gráfica anterior de un ACLR(5,h), se observa que partiendo de las clases unitarias (1,2,4,8,16), todas las rutas "suben" hasta el nivel máximo o "bajan" al conjunto vacio, en este caso tendríamos que R=5, podemos conocer el índice L tomando la reflexión de la regla de evolución original, esto es las vecindades de la regla de evolución con valores asimétricos se intercambian para reflejar la regla de evolución como un espejo, el efecto que tiene la reflexión de la regla original es convertir los conjuntos compatibles por la izquierda en conjunto compatibles por la derecha, si observamos ahora el diagrama de subconjunto de la reflexión de la regla estaremos conociendo su índice L.
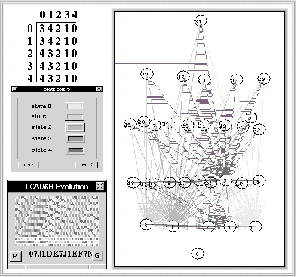
Figura: ACLR(5,h) reflexión de la regla 000667CCIJOOI y su diagrama de
subconjuntos.
En este ejemplo se observa que el diagrama de subconjuntos carece de rutas del
subconjunto total al conjunto vacio, todas las rutas tienden a subconjuntos con los
valores de L=1 en la reflexión obteniendo que 
para el ACLR(5,h).
Para saber por medio del diagrama de subconjuntos si un ACL es reversible, por
principio de cuentas no debe existir una ruta que vaya desde el subconjunto máximo al
conjunto vacio, en el diagrama de la regla original toda ruta que parta desde las clases
unitarias de llegar a un nivel de subconjuntos con cardinalidad R y nunca salir de
este nivel sin ciclos intermedios entre el nivel unitario y el nivel R, lo mismo
debe ocurrir para la reflexión de la regla de evolución ahora partiendo desde los
subconjuntos unitarios y terminando en un nivel con cardinalidad L sin ciclos
intermedios entre el nivel unitario y el nivel L, donde 
.