Sabemos que los nodos en el diagrama de parejas son pares de nodos del diagrama de de
Bruijn, y existe una liga del nodo 
al nodo 
si los elementos del nodo 
se conectan con la misma liga con los elementos del nodo 
en el diagrama de de Bruijn, tomando esta idea
tenemos que la diagonal principal del diagrama de parejas no es más que el mismo diagrama
de de Bruijn base.
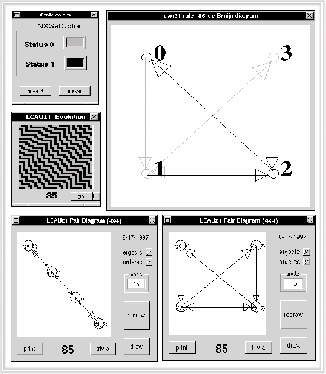
Figura: ACLR(2,1) regla 85 y su diagrama de parejas asociado.
En el esquema se observa un ACLR(2,1) regla 85 y su diagrama de de Bruijn así como la diagonal principal aislada de su diagrama de parejas, en la cual se volvieron a reacomodar sus nodos para mostrar que tiene la misma estructura que el diagrama de de Bruijn.
Sin embargo, si existen ciclos fuera de la diagonal principal del diagrama de parejas indica que dentro del diagrama de de Bruijn una misma cadena puede generarse de varias formas distintas, o sea que tiene más de un ancestro posible lo que indica que el ACL no es reversible.
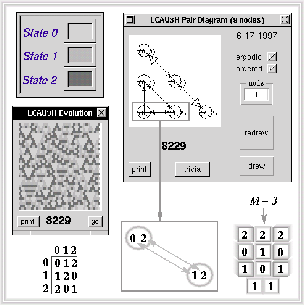
Figura: ACLR(3,h) regla 8229 y su diagrama de parejas asociado.
En este ejemplo la cadena de estados 11 puede ser producto de la evolución de las extensiones compatibles por ambos lados ya sea de 0, 1 o 2, es decir M=3, ésto se observa claramente en el ciclo señalado en el diagrama de parejas que nos indica que dicha cadena tiene ancestros múltiples impidiendo que el ACL sea reversible.
Lo que nos muestra el diagrama de parejas es si existe una cadena de estados que tenga varios ancestros, es decir si la regla de evolución del ACL define un mapeo global inyectivo o no.