David Hillman [10] desarrolla un algoritmo para detectar todos los posibles ACLR con culaquier número de estados y cualquier tamaño de vecindad, el proceso es el siguiente:
Se van formando todos los posibles ancestros 
de una cadena y de tamaño w y se almacenan en una tabla las parejas
formadas por los 2r elementos iniciales y finales de cada 
, esto se hace para cada posible y, al final se tendran un
conjunto de tablas que guardan los 2r elementos iniciales y finales de los posibles
ancestros de cada cadena de ancho w, a tal conjunto se le denominará 
; se empieza con w=1, para valores de w>1
simplemente se concatena 
con 
comparando cada tabla de 
con cada tabla de 
, si 2r elementos
finales de la tabla en 
son iguales a los 2r
elementos iniciales de la tabla en 
entonces se
añade una nueva entrada en la tabla de 
formada
por los 2r elementos iniciales en la tabla de 
y los 2r elementos finales en la tabla de 
, las tablas de 
se obtienen
directamente de la regla de evolución, de esta manera el proceso puede ser implementado
en una computación recursiva; si el ACL es reversible, debe existir para cada tabla en 
una sola pareja en donde los 2r elementos
iniciales sean iguales con los 2r elementos finales ya que esto indicaría que una
y solo una cadena 
de longitud w puede
evolucionar en y para toda y de longitud w, es decir, cada posible
cadena solo tendría un único ancestro y por lo tanto su evolución sería invertible.
Por supuesto, si w es grande el método se vuelve muy laborioso, sin embargo
Hillman hace dos observaciones que minimizan este problema; en primera si la tablas de un
conjunto 
no tienen todas el mismo número de
parejas entonces el ACL no es reversible pues este desequilibrio llevará a que la
información del sistema se pierda gradualmente y con esto la reversibilidad del mismo; el
segundo punto que Hillman señala es que como los valores que pueden tener cada tabla son
finitos, entonces llegará un momento en que se repetirán estos valores; en síntesis, si
cada tabla en 
tiene el mismo número de parejas
para 
y 
para i<j entonces el ACL es reversible y el proceso termina.
Veamos un ejemplo de este algoritmo para ACL(3,h).
Formemos las tablas de los 2r elementos iniciales y finales para los ancestros de 0, 1 y 2.
Tabla: Conjunto 
para el
ACL(3,h) regla 6007.
Para 
se encuentra que cada posible cadena
tiene un solo ancestro, ahora concatenemos 
consigo mismo para obtener los ancestros de 00, 01 y 02.
Como no se cumple la condición de que cada tabla tenga el mismo número de parejas, se detiene el algoritmo y ACL(3,h) no es reversible.
Veamos otro ejemplo para otro ACL(3,h).
Formemos las tablas de los 2r elementos iniciales y finales para los ancestros de 0, 1 y 2.
Tabla: Conjunto 
para el
ACL(3,h) regla 14007.
Para 
también encontramos que cada posible
cadena tiene un solo ancestro, ahora concatenemos 
consigo mismo para obtener los ancestros de 00, 01 y 02.
Aquí se observa que la cadena 00 tiene tres posibles ancestros mientras que las cadenas 01 y 02 no tienen ninguno, así que se detiene el algoritmo y ACL(3,h) no es reversible.
Veamos otro ejemplo para otro ACL(3,h).
Formemos las tablas de los 2r elementos iniciales y finales para los ancestros de 0, 1 y 2.
Tabla: Conjunto 
para el
ACL(3,h) regla 2119.
Para 
también encontramos que cada posible
cadena tiene un solo ancestro, ahora concatenemos 
consigo mismo para obtener los ancestros de todas las posibles cadenas de longitud 2, en
este caso solo obtenemos tres tablas distintas las cuales son:
Si concatenamos ahora 
con 
obtenemos:
Como este conjunto es igual a 
, tenemos que el
ACL(3,h) es reversible y se detiene el proceso.
En resumen, el algoritmo de Hillman va formando todos los posibles ancestros de las cadenas de longitud w empezando desde 1 y checa si hay un único ancestro para cada una de estas cadenas de longitud w+2r que al tener los elementos 2r iniciales y finales iguales, se pueda representar como una secuencia de estados también de longitud w que evoluciona en la cadena estudiada.
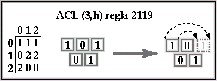
Figura: Ancestro único de la cadena 01 que puede representarse
con la misma longitud.
con 
.
con 
.
.
.