![]()
Una aproximación tentativa en tratar de utilizar los resultados de los trabajos en [9] y [16] fué desarrollada por el Dr. Harold V. McIntosh y Jose Manuel Gómez Soto; este algoritmo consiste en aprovechar los conceptos de multiplicidad uniforme e índices de Welch para la construcción de las posibles matrices de evolución de ACLR; por ejemplo, para un ACLR(5,h) se tiene la siguiente ``plantilla'' para generar las matrices de evolución:

Tabla: Plantilla para generar matrices de evolución de ACLR(5,h).
El resto de los lugares vacios se llenaban con todas permutaciones de estados posibles de tal manera que un elemento de cada columna fuera diferente al resto, esto es ya que al tener cinco nodos el diagrama de de Bruijn asociado, el valor de LMR=5, por lo que se fija a M=1 y L=1, lo que implica que no debe existir dos elementos iguales por columna.
La razón por la cual el último renglón de la matriz estaba lleno del estado 4 era para tener un estado en el cual fuera seguro que el conjunto de todas sus extensiones compatibles derechas tuviera una cardinalidad igual a R, cumpliendo para ese estado que LMR=5, una vez llena la matriz, se generaba una evolución de este ACL y se observaba si cada posible vecindad de longitud 2 tenía un único estado para el cual evolucionar hacia atrás, de cumplir ésto, el ACL se tomaba como reversible, de no ser así se verificaban si las vecindades de longitud 3 si cumplían con tener un único estado en el pasado; este proceso continuaba hasta revisar vecindades de longitud 4.
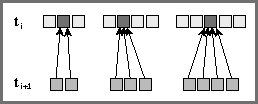
Figura: Verificación de que cada cadena tenga un único elemento en
común en el pasado para cadenas de longitud 2, 3 y 4.
La ventaja de este planteamiento es que ya no hace la revisón de cada posible regla de evolución para un ACL(k,h) sino que solo analiza aquellas matrices de evolución en donde se tenga una diagonal principal donde cada estado sea diferente al resto y un renglon formado por un mismo valor para asegurar que la cardinalidad del conjunto de extensiones compatibles por la derecha del mismo fuera R, con lo que el tiempo de computación que toma hacer el cálculo se reduce de manera significativa.
![]()