Un ACL se construye de la siguiente manera; se coloca una serie de celdas en línea, es decir un arreglo lineal de elementos los cuales se denominan células.
Cada célula puede tener un número finito de valores, ya sea un valor entero, una letra o un color, lo que se quiera que represente cada una, a estos valores se les denomina estados, todas las células tienen el mismo número posible de estados.
Las relaciones que existe entre las células constituyen los tipos de vecindades que forman, se puede tomar para una célula dada un radio de vecindad r, es decir r vecinos a cada lado de la misma, obteniendo un tamaño de vecindad igual a 2r+1, el número total de células que forman la vecindad.
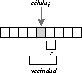
Figura: ACL donde cada célula tiene un vecino a cada lado (r=1),
el tamaño total de la vecindad es 2r+1=3.
En los extremos del arreglo la célula inicial y final no tienen el mismo vecindario que las células interiores, por ésto para preservar la uniformidad de todos los vecindarios, la cadena puede ser imaginada como un anillo, así la primera célula del arreglo es la vecina derecha de la última y ésta es la vecina izquierda de la primera.
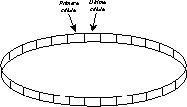
Figura: Cadena de células dispuesta en forma de anillo.
Wolfram propone una notación para los ACL, la cual es 
, es decir existen k estados posibles para cada célula junto con r
células de cada lado para formar su vecindario, por ejemplo, para un ACL(2,1) el
vecindario contiene tres células y cada célula puede tener un estado de dos posibles, el
número posible de vecindades diferentes es 
, en
este caso 
, si los estados posibles fueran 0,1,
las vecindades que tendríamos serían 
.