Commentary related to Andrew Wuensche and Mike Lesser's book, ``The Global Dynamics of Cellular Automata.'' Addison-Wesley, 1992 (ISBN 0-201-55740-1) continues. At least two different parameters, lambda and Z, are useful in classifying cellular automata; but the general philosophy of parameters should be contemplated before deciding to rely on one or another of them, or on something else.
It is a natural idea to assign a single number to an automaton, or to an automaton rule, with the expectation that it will distinguish between automata, and perhaps also reveal some significant information about them. An extremely natural and obvious candidate is the fraction of transitions (or neighborhoods, if you wish) leading to one of the states, particularly in a binary automaton.
From the side of probability theory, one expects an automaton to evolve into an equilibrium in which the fraction of neighborhoods producing the state is the same as the relative proportion of that state. In its simplest application, this is mean field theory, but other approaches utilize varying degrees of sophistication for estimating the probabilities, making for correspondingly better estimates. The fraction of neighborhoods serves as an excellent starting point for these theories, and is often not too far from the equilibrium calculated by other theories.
From the side of ancestor theory, we have seen that there are some matrices arising from graph theory, whose spectral radii and spectral norms, between them, account for the proliferation of ancestors, which is the converse of the convergence seen during evolution. We have also seen that the ancestor fraction serves to give a reasonable estimate of the growth rate, not of ancestors from generation to generation, but of the number of ancestors for a single generation as a function of the length of a configuration.
Indirectly these estimates affect the characteristics of the evolution for many generations, which are thereby related to the underlying parameter. Thus a parameter may serve for more than classification, it may participate in some simple algabraic expression describing observable data produced by the automaton. When a parameter enjoys a general display of success, the public seems to become more demanding in its expectations for the parameter, requiring either a new and better parameter, or some supplementary parameters which explain discrepancies in the predictions of the original paramenter.
With respect to the calculation of ancestors, there is a good and solidly based theory from which to start. The de Bruijn diagram, and such of its subsidiaries as the subset diagram, pair diagram, union diagram, and so on, allow an exact calculation of ancestors, and statistics of ancestors, such as their average number, standard deviation, and, through their moments, their exact frequency distribution. In practice, the matrices are large, the calculations tedious, and above all, symbolic results are desired which apply to whole classes of automata, rather than just individual cases.
The procedure would be easier were it not for the discrepancy between spectral norm and spectral radius, but in general terms, estimating the largest eigenvalue of the larger of the de Bruijn fragments is sufficient to estimate the largest number of ancestors that any single configuration can possibly have, which is a quantity of interest that is tabulated in the Atlas.
The average number of ancestors is always necessarily 4, for (2,1) automata, but the actual number is influenced, especially for configurations of short length, by boundary conditions, and by the variance, which can be estimated by the same procedures using another matrix (the pair matrix). The actual distribution is highly skewed, because half of the configurations, in some sense, have 4 or less ancestors. This quantity includes zero ancestors - Garden of Eden configurations - and is just as inevitable as the average of 4.
Not only is the top half of the distribution highly skewed - spread over
the range 
- but it typically contains a few outliers with the
bulk of the data closer to the mean; the standard deviation has to take
this into account.
The outliers are generally the ancestors of the quiescent state, if there IS one. Modifications in this observation have to be made when there are TWO quiescent states, or none, or the state with the majority of ancestors is not the quiescent state (for non-binary automata the permutations increase quite rapidly with the number of states).
In previous commentaries, we have shown that both Langton's lambda and
Wuensche and Lesser's Z can be incorporated into formulas expressing the
rate of growth of ``maximal preimaging'' (beware - 
is 
and |em vice versa).
There is nothing especial to reccomeend these formulas except that they are extremely simple; in the Langton version, the second term is simply ignored. Nevertheless the results agree to about 10%, while the accurately computed eigenvalues agree quite well with data taken from the Atlas.
To satisfy curiosity regarding the composition of the discarded term, it is tabulated below for the ab values 08, 17, 26, and 35, according to Wuensche and Lesser's clusters, all of whose members obey the same statistics.
0.50em
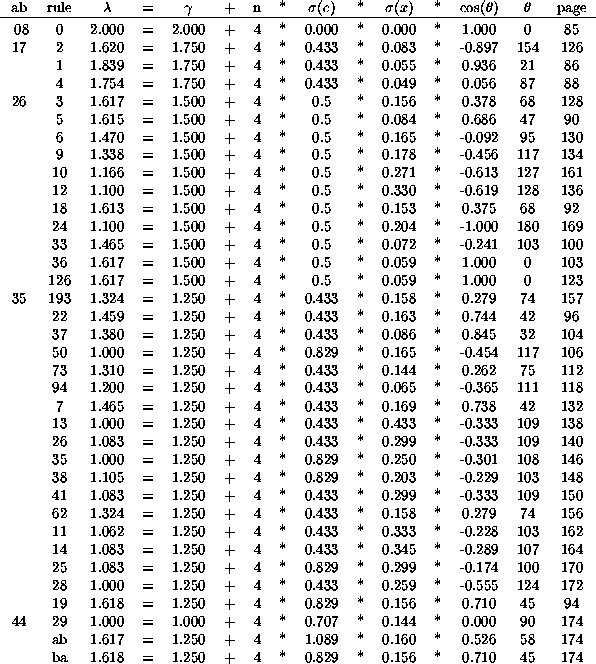
In earlier commentaries, we have remarked on the excellent agreement between the eigenvalues and data in the Atlas. Even the three 26 cases which were judged to be marginal conform quite well to the predictions; we were much too hasty in our earlier conclusion, due to the large number of small basins and the closeness of the growth factors to 1.0.
Nevertheless, the agreement begins to suffer with the 35 and 44 automata, for reasons which answer an earlier question. 44 is balanced, yet does not always produce zero variance (a known failing). The answer is that the de Bruijn fragments can be strongly attractive and dissipative, hence the matrix might have the Jordan form, and the eigenvalue could differ markedly from the spectral norm.
It will be seen that the products AB and BA behave better than A or B alone, giving maximal preimaging consistent with the configurations 01010101.... shown in the Atlas, whilst the chains 0000... and 1111... may have rather few counterimages.
The single 44 example in the table illustrates what has happened. The spectral
norm of the fragments is sqrt(2) = 1.414, but their eigenvalue is 1. While the
eigenvalue underestimates general growth rates, the spectral norm overestimates
them, given that the true result is 
.
More commentary will follow.