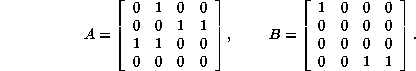
Commentary related to Andrew Wuensche and Mike Lesser's book, ``The Global Dynamics of Cellular Automata.'' Addison-Wesley, 1992 (ISBN 0-201-55740-1) continues. The time has come to investigate Z.
We are basing our commentary on the A and B matrices into which the de Bruijn connectivity matrix for any binary rule splits. Consider Rule 193, featured in the text on page 40 of the Atlas; its AB pair is:
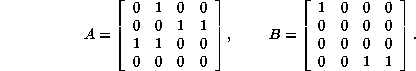
For A, the vector of column sums is (1 2 1 1), of row sums it is (1 2 2 0).
The column average is 5/4 = 1.25, the second moment is 7/4 = 1.75, giving a
. For rows the average is also 5/4 = 1.25, with second
moment 9/4 = 2.25 and 
approximately. Using columns seems
preferable.
Earlier we stated a 'Statistical Gershgorin Theorem' (erroneously writing var for the greek sigma that was in the original source):
where lambda is an eigenvalue (NOT Langton's parameter) of a matrix such as
A, 
is 
the sum of the elements of the matrix (and IS double
Langton's parameter when the majority state is quiescent). N is the number
of rows in the matrix, here 4, the sigmas refer respectively to column sums
and the eigenvector, and 
is the angle between their vectors of
residuals. Interestingly, this angle must be EXACTLY 90 degrees for reversible
automata
.
Up until now, we have drawn some conclusions based on using 
while
discarding the companion term; but all discrepancies noted are exclusively
due to the correction. The discrepancies seem to follow a regular pattern,
small but typically non-zero.
It will be noted that the A and B matrices have three kinds of rows (and columns as well). They can be zero, unit vectors, or contain a pair of ones. The general format is forced by the structure of the de Bruijn diagram, being just the number of out links (in links) per start string (stop string). Given more states than a binary automaton possesses, there will be more links, and so a greater variety of rows or columns; but the unit vectors signal situations in which just one single continuation is possible.
The unit vectors are significant, being what the Atlas calls deterministic; the fraction of them taking both A and B into consideration is Z. One is allowed to choose between rows or columns, so as to get the larger of the two numbers.
For Rule 193, there are altogether 2 unit rows and 6 unit columns. Therefore Z = 6/8, or 0.75, whereas the (Langton's) lambda is 5/8, or 0.625, yielding the lambda ratio 0.75 duly recorded in the Atlas, page 157.
Estimating the largest eigenvalue of A produces 1.324, which can be compared to the quotient of maximum preimaging for 15 and 14 member rings (p. 157), which is 68/51 = 1.333. Again, the agreement is exemplary.
Comparing fairly modest powers of A reveals the eigenvectors of this eigenvalue; normalized they are: column, (0.246, 0.323, 0.430, 0.000), row, (0.184, 0.323, 0.246, 0.246).
Residuals for the column sum are (-0.25, 0.75, -0.25, -0.25), residuals
for the column eigenvector are (-0.004, 0.073, 0.180, -0.250). The inner
product of these two vectors give directly the correction to 
, and
is 0.072. Almost exactly what is expected, 1.250 + 0.072 = 1.322, the tiny
discrepancy is surely due to the care (or lack thereof) taken in arriving
at these numbers.
The 
norm of zero-average vectors is their standard deviation without
averaging, which accounts for the factor n in the statistical theorem, so
we quickly arrive at a value of 
of 0.271, or a 
of
about 74 degrees. We already knew 
; we readily calculate
, so we have identified all the quantities in the formula.
There is an interesting, although possibly trivial, way to place Z in this formula. Create the supermatrix from A and B that was once mentioned:
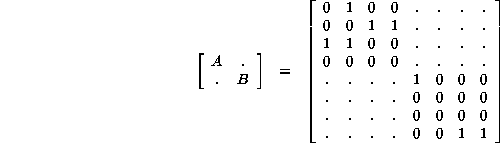
It is not such an artificial creation as might be feared: from graph theory it is the connectivity matrix of the least upper bound (union) of two graphs; one is the de Bruijn diagram with 0-ancestor links, the other is the de Bruijn diagram with 1-ancestor links. Nodes in a union are linked when there are links in either one (or both) of its two constituents.
The vector of column sums is (1 2 1 1 1 0 1 1). The average of column sums
is 1, composed from 0's, 1's, and 2's; every 0 is paired with a 2. Thus the
vector of residuals, (0 1 0 0 0 -1 0 0) will contain -1's, 0's, and 1's; the
sum of their squares will be eight minus the number of columns which were unit
vectors, so the average of the sum is 1-Z. Sigma squared is the second moment
taken with respect to residuals, so 
. When Z=1, as for
reversible Rules, the standard deviation is zero; when Z=0, as for the Zero
Rule, the standard deviation is 1.
The supermatrix now encompasses both maximum and minimum rates of growth;
being partially diagonal its eigenvectors are those of its blocks, extended
to the other block with zeroes, and the statistical theorem still applies to
all eigenvalues. Because of the increased dimension, each eigenvector will
be the same as before, but its mean will be reduced by half (to 1/8) because
of all the new zeroes, while its second moment 
will be shifted by 1/64
and scaled by 1/2. Finally, the supermatrix has eight rows and always has
eight ones distributed throughout. So the new formula is
where we still have to contend with a new angle 
whose cosine we
calculate to be 0.482 (about 61 degrees). The equality is nearly as good,
Just as the extended eigenvector is gotten by filling with zeroes, the
extended vector of sums is gotten by adjoining 2u-x (making for the average
of 1 and variance 1-Z), where u is a vector of 1's and x is the vector to be
extended. The extended vectors of the Union Matrix therefore have the same
inner product as the original vectors. Nevertheless, the residual vectors,
from which 
is calculated, are slightly different; anyone who
wanted an explicit relation between 
and 
could work out
the algebra.
Critics may question the utility of the formulas that have been displayed; it remains to be seen to what extent the standard deviations and angles are consistent within families of automata, or whether they can be transferred from one automaton to another.
Nevertheless we have constructed a framework into which Langton's parameter and Z both fit, as algebraic quantities relating to the growth factor for maximal counterimaging.
More commentary will follow.