Commentary related to Andrew Wuensche and Mike Lesser's book, ``The Global Dynamics of Cellular Automata.'' Addison-Wesley, 1992 (ISBN 0-201-55740-1) continues. Having described the line of reasoning leading to the Uniform Multiplicity Theorem, we turn to an analysis of variance, or equivalently, of the second moment of the ancestor distribution. The reason for the interest lies in the relation between zero variance and zero Garden of Eden.
Every (2,1) automaton has a pair of 4x4 matrices which can be used to
count ancestors and whose tensor squares count squares of numbers of
ancestors; these are the A and B matrices of previous commentaries.
Individual terms in the expansion of 
yield the number of ancestors
associated with the monomials in the expansion; A+B itself is the de Bruijn
matrix D, whose powers can be calculated explicitly. Each one is double its
predecessor, and in the end there is an AVERAGE of four ancestors per
configuration, whatever its length. How well individual terms of the sum
conform to this average is an object of study.
For the second moment, powers of 
are required; this is
not the same as 
; and therein lies a tale. What we need are
eigenvalues, not forgetting the discrepancy between spectral norm and spectral
radius for certain matrices. A widely used, and one of the best, estimates of
the eigenvalues of a matrix is Gerschgorin's theorem, which has some
alternative forms. One says that the eigenvalue is contained in a disk
in the complex plane whose radius is the sum of the absolute values of
the elements of some row. Not knowing which row leads to superposing the
disks for each row and saying that the eigenvalue is lurking somewhere
within. All of them.
Obvious variants use columns instead of rows, others center the disk on the (complex) diagonal elements, calculating the radius from the remainder of the row. It is also possible to average the rows, and it is possible to apply statistical concepts to the rows and eigenvectors themselves. Here it is useful to work with non-negative matrices, because all the numbers in the matrices can be used directly without absolute values. Furthermore, the eigenvector whose eigenvalue dominates the growth rate is non-negative, or can be normalized to be so.
Elementary statistics teaches that the average is an ideal origin for a set
of data, within which the variance provides an ideal scale. Following this
precept, the elements of a vector might be decomposed into an an average
plus a residual. Write the column sums in a matrix as 
, the
normalized eigenvector as 
(for an nxn matrix), whose Perron
eigenvalue (the largest one) is 
. Then there is a Statistical
Gershgorin Theorem which asserts
where 
is an angle involved in the derivation (correlation between c
and x), but whose cosine is bounded between -1 and 1. For the matrices of our
interest, 
is 1/n th the sum of their elements. For A and B, this is 1/4
the number of ancestors, and so a number ranging between 0 and 2. For
, 
, and their sum, we have 1/16 the square of the
number of ancestors. For 
and 
, the value ranges
between 0 and 4 (the square of 2), while for 
it
ranges between 2 and 4.
Of the correction terms in this formula, n can be large, the variance in
column sums can be modest; and the variance in x is small, the elements
themselves never surpassing 1 and averaging 1/n. The formula itself is not
something that anyone would think remarkable, and one mostly hopes that
either the variances are small or that 
runs around 90 degrees. On
the other hand, when the correction IS minor, it says that an 'average'
number of ancestors is the eigenvalue which determines the growth rate.
Suppose that a is the sum of the elements in A, and b is the sum of the
elements in B. We have a+b=8 always. To estimate the eigenvalue of
, we would then have 
, subject to the
same constraint. The value is smallest when a=b, greatest when a=0 or b=0,
symmetric between a and b.
The following table summarizes the results of a survey in which the maximum eigenvalue of each matrix was estimated by comparing the ratio of its third and fourth powers. The data was classified according to the value of a, with averages and variances for the estimated eigenvalue calculated individually for each value of a.
In addition, the value for a=b (44) was split into two groups, according to whether the eigenvalue was 2 or not.
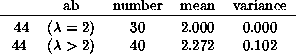
The number in each of these categories is a binomial coefficient.
One may judge how well the estimate of 
matches the experimental data.
It seems mostly better than 5%, and often better than 1%.
To turn the second moment into a variance, we need the relationship
Since the average is 2, and the second moment lies in the range 2-4,
the standard deviation lies in the range 0-sqrt(2), with the assurance
that some data are actually as far away from the mean as the standard
deviation. Tchebycheff's Theorem is also pertinent, that less than 
of the data lies more than f standard deviations away from the mean.
The members of the group of 30 in the last table are candidates for reversible rules, and are the only (2,1) Rules for which there is no Garden of Eden. The other 40 Rules in the 44 class are balanced, in the sense that a=b and 0 has as many ancestral neighborhood as 1, namely 4 out of 8. That requirement is necessary but not sufficient.
The data which has been tabulated and discussed can also be presented as a histogram, but the limitations of a typescript prevent showing it on a printed page (although we could no doubt create an acceptable image if we really tried).
These results have been taken from two preprints which can be had upon request (with full mailing address), and were obtained by the use of the program LCAU21, for PC's, which is also available on request. Using it is non-trivial, however, due to its meagre documentation, especially in the ancestor option.
More commentary will follow.