


Siguiente: Algorithms for field arithmetic
Arriba: Field operations with the
Anterior: Multiplication
Also, in terms of a primitive element
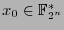 we may express the elements of
we may express the elements of
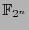 through the map
through the map
![$J: \mathbb{F}_{2^n}\to[\![0,2^n-1]\!]$](img70.png) such that
such that 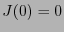 and
and
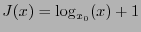 . For any
. For any
![$i,j\in[\![0,2^n-2]\!]$](img78.png) , with
, with 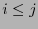 , we have
, we have
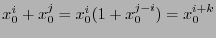 , where the addition is taken modulus
, where the addition is taken modulus 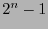 and
and
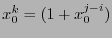 , or
, or
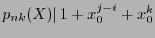 .
Thus, addition involves the irreducible polynomial
.
Thus, addition involves the irreducible polynomial 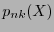 .
The corresponding form of addition for
.
The corresponding form of addition for 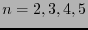 are displayed in tables 22-26.
are displayed in tables 22-26.
Table:
Logarithmic addition table in
![$[\![0,2^2-1]\!]$](img21.png) using map
using map 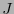 .
.
 |
 |
|
(a) |
(b)
|
|
Table:
Logarithmic addition table in
![$[\![0,2^3-1]\!]$](img23.png) using map
using map 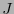 .
.
 |
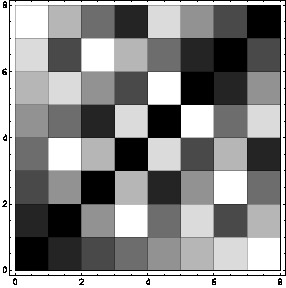 |
|
(a) |
(b)
|
|
Table:
Logarithmic addition table in
![$[\![0,2^4-1]\!]$](img25.png) using map
using map 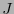 .
.
 |
(a)
|
 |
|
(b)
|
|
Table:
Logarithmic addition table in
![$[\![0,2^5-1]\!]$](img26.png) using map
using map 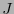 (numeric values).
(numeric values).
 |
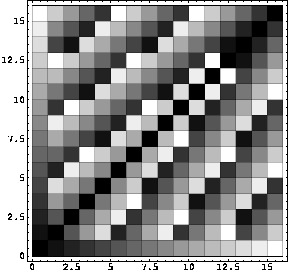
Table:
Logarithmic addition table in
![$[\![0,2^5-1]\!]$](img26.png) using map
using map 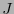 (density plot).
(density plot).
|



Siguiente: Algorithms for field arithmetic
Arriba: Field operations with the
Anterior: Multiplication
Guillermo M. Luna
2010-02-19
![]() we may express the elements of
we may express the elements of
![]() through the map
through the map
![]() such that
such that ![]() and
and
![]() . For any
. For any
![]() , with
, with ![]() , we have
, we have
![]() , where the addition is taken modulus
, where the addition is taken modulus ![]() and
and
![]() , or
, or
![]() .
Thus, addition involves the irreducible polynomial
.
Thus, addition involves the irreducible polynomial ![]() .
The corresponding form of addition for
.
The corresponding form of addition for ![]() are displayed in tables 22-26.
are displayed in tables 22-26.