


Siguiente: Addition
Arriba: Field operations with the
Anterior: Field operations with the
The multiplication group
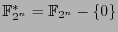 of the Galois field
of the Galois field
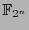 is cyclic, hence for any primitive element
is cyclic, hence for any primitive element
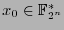 we have that for all
we have that for all
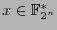 there is a
there is a
![$y\in [\![0,2^n-2]\!]$](img66.png) such that
such that 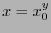 . Obviously, it is written
. Obviously, it is written
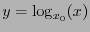 . Through this function, the multiplication can be expressed additively:
. Through this function, the multiplication can be expressed additively:
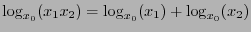 . Let
. Let
![$J: \mathbb{F}_{2^n}\to[\![0,2^n-1]\!]$](img70.png) be the map such that
be the map such that 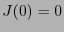 and
and
 . Hence
. Hence  is a bijection and the multiplication in
is a bijection and the multiplication in
 determines an operation
determines an operation
![$*:[\![0,2^n-1]\!]\times[\![0,2^n-1]\!]\to[\![0,2^n-1]\!]$](img73.png) , which is the multiplication using the discrete logarithm representation.
These operations are displayed in tables 17-21.
, which is the multiplication using the discrete logarithm representation.
These operations are displayed in tables 17-21.
Table:
Logarithmic multiplication table in
![$[\![0,2^2-1]\!]$](img21.png) using map
using map  .
.
 |
 |
|
(a) |
(b)
|
|
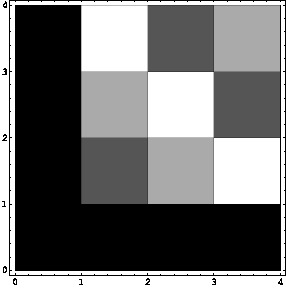
Table:
Logarithmic multiplication table in
![$[\![0,2^3-1]\!]$](img23.png) using map
using map  .
.
 |
 |
|
(a) |
(b)
|
|
Table:
Logarithmic multiplication table in
![$[\![0,2^4-1]\!]$](img25.png) using map
using map  .
.
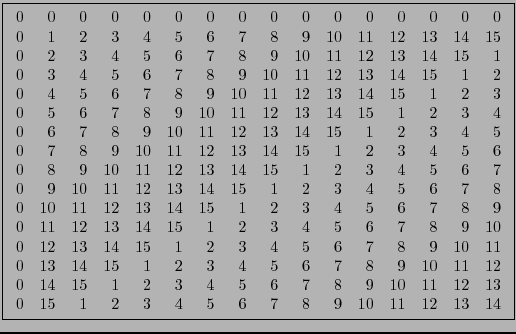 |
(a)
|
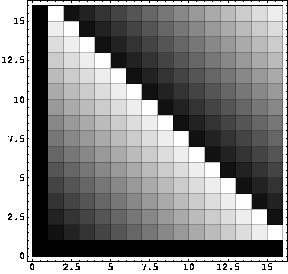 |
|
(b)
|
|
Table:
Logarithmic multiplication table in
![$[\![0,2^5-1]\!]$](img26.png) using map
using map  (numeric values).
(numeric values).
 |
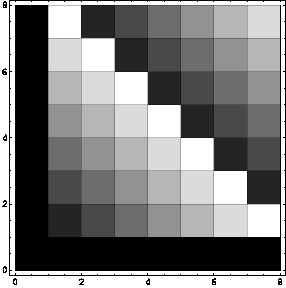
Table:
Logarithmic multiplication table in
![$[\![0,2^5-1]\!]$](img26.png) using map
using map  (density plot).
(density plot).
|

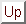


Siguiente: Addition
Arriba: Field operations with the
Anterior: Field operations with the
Guillermo M. Luna
2010-02-19
![]() of the Galois field
of the Galois field
![]() is cyclic, hence for any primitive element
is cyclic, hence for any primitive element
![]() we have that for all
we have that for all
![]() there is a
there is a
![]() such that
such that ![]() . Obviously, it is written
. Obviously, it is written
![]() . Through this function, the multiplication can be expressed additively:
. Through this function, the multiplication can be expressed additively:
![]() . Let
. Let
![]() be the map such that
be the map such that ![]() and
and
![]() . Hence
. Hence ![]() is a bijection and the multiplication in
is a bijection and the multiplication in
![]() determines an operation
determines an operation
![]() , which is the multiplication using the discrete logarithm representation.
These operations are displayed in tables 17-21.
, which is the multiplication using the discrete logarithm representation.
These operations are displayed in tables 17-21.