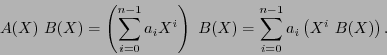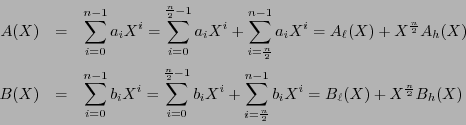


Siguiente: Squaring
Arriba: Algorithms for field arithmetic
Anterior: Algorithms for field arithmetic
Let
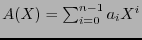 and
and
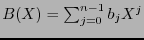 be two elements in
be two elements in
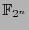 expressed with respect to the polynomial basis. Then
expressed with respect to the polynomial basis. Then
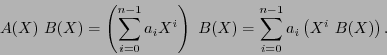 |
(1) |
Besides,
Clearly, eq's (1)-(3) determine an algorithm to compute the multiplication.
As a second procedure, let us recall the famous Karatsuba-Ofman. Let us split the factors as
where
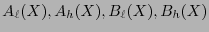 are polynomials of degree
are polynomials of degree 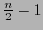 . Thus
. Thus
Eq. (4) determines a divide-and-conquer algorithm for multiplication. If 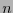 is a power of 2,
is a power of 2, 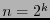 , and
, and 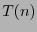 counts the number of
counts the number of 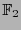 -operations to perform the multiplication in
-operations to perform the multiplication in
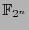 then the following recursion results from (4):
then the following recursion results from (4):
and its solution is 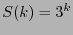 , namely
, namely
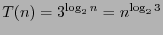 , thus the ratio
, thus the ratio
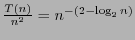 tends to 0 as
tends to 0 as
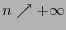 .
.



Siguiente: Squaring
Arriba: Algorithms for field arithmetic
Anterior: Algorithms for field arithmetic
Guillermo M. Luna
2010-02-19