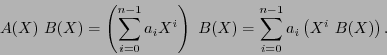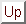
Siguiente: Squaring Arriba: Algorithms for field arithmetic Anterior: Algorithms for field arithmetic

Multiplication

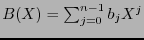Let $A(X)=\sum_{i=0}^{n-1}a_iX^i$ and $B(X)=\sum_{j=0}^{n-1}b_jX^j$ be two elements in 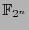$\mathbb{F}_{2^n}$ expressed with respect to the polynomial basis. Then

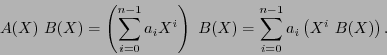$$A(X)\ B(X) = \left(\sum_{i=0}^{n-1}a_iX^i\right)\ B(X) = \sum_{i=0}^{n-1}a_i \left(X^i\ B(X)\right).$$ (1)

Besides,

$$X^{i+1}\ B(X) = X(X^i\ B(X)) \hspace{3em} \mbox{ and}$$ (2)

$$X\ B(X) = X\sum_{j=0}^{n-1}b_jX^j = b_{n-1}X^n+ \sum_{j=1}^{n-1}b_{j-1}X^j = b_{n-1}q_0 +\sum_{j=1}^{n-1}\left[b_{j-1}+b_{n-1}q_j\right]X^j.% \\$$ (3)

Clearly, eq's (1)-(3) determine an algorithm to compute the multiplication.

As a second procedure, let us recall the famous Karatsuba-Ofman. Let us split the factors as

$$\begin{eqnarray*} A(X) &=& \sum_{i=0}^{n-1}a_iX^i = \sum_{i=0}^{\frac{n}{2}-1}a_... ...\frac{n}{2}}^{n-1}b_iX^i = B_{\ell}(X) + X^{\frac{n}{2}} B_h(X) \end{eqnarray*}$$

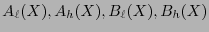where $A_{\ell}(X) , A_h(X),B_{\ell}(X) , B_h(X)$ are polynomials of degree 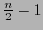$\frac{n}{2}-1$. Thus

$$A(X)\ B(X) = \left(A_{\ell}(X) + X^{\frac{n}{2}} A_h(X)\right) \left(B_{\ell}(X) + X^{\frac{n}{2}} B_h(X)\right)$$

$$= A_{\ell}(X)B_{\ell} + \left(A_{\ell}(X) B_h + A_h(X) B_{\ell}(X)\right)\ X^{\frac{n}{2}} + A_h(X) B_h(X)\ X^{n-1}$$

$$= A_{\ell}(X)B_{\ell}$$

$$+ \left[ \left(A_{\ell}(X) + A_h(X)\right)\left(B_{\ell}(X) + B_h(X)\right) + A_{\ell}(X)B_{\ell}+ A_h(X) B_h(X) \right]\ X^{\frac{n}{2}}$$

$$+ A_h B_h(X)\ X^{n-1}%\\$$ (4)

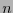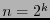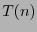Eq. (4) determines a divide-and-conquer algorithm for multiplication. If $n$ is a power of 2, $n=2^k$, and $T(n)$ counts the number of 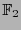$\mathbb{F}_2$-operations to perform the multiplication in 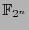$\mathbb{F}_{2^n}$ then the following recursion results from (4):

$$S(k)=T(n)=3T\left(\frac{n}{2}\right)=3S(k-1)\ \ \ ,\ \ \ S(0)=T(1)=1,$$

and its solution is 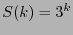$S(k)=3^k$, namely 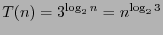$T(n)=3^{\log_2n}=n^{\log_23}$, thus the ratio 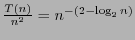$\frac{T(n)}{n^2}=n^{-(2-\log_2n)}$ tends to 0 as $n\nearrow +\infty$.

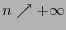Siguiente: Squaring Arriba: Algorithms for field arithmetic Anterior: Algorithms for field arithmetic