


Siguiente: Square root
Arriba: Algorithms for field arithmetic
Anterior: Multiplication
Since
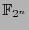 is a field of characteristic 2, squaring is a linear map, thus
is a field of characteristic 2, squaring is a linear map, thus
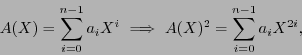 |
(5) |
thus only monomials of even exponent appear in 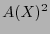 .
.
If 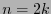 is an even number,
is an even number,
If 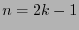 is an odd number,
is an odd number,
Eq's (6)-(7) determine an algorithm for squaring, which can still be simplified, according to the special form of the irreducible polynomial 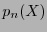 .
.
Guillermo M. Luna
2010-02-19
![]() is a field of characteristic 2, squaring is a linear map, thus
is a field of characteristic 2, squaring is a linear map, thus
![]() is an even number,
is an even number,